Объяснение:
Чтобы решить эту задачу, нужно знать как минимум 2 операции с матрицами:
Сложение/вычитание матриц. Если у тебя есть матрица A с элементами (т.е. на i строке j столбца находится число
(т.е. на i строке j столбца находится число  ), и некоторая другая матрица той же размерности B с элементами
), и некоторая другая матрица той же размерности B с элементами  , то в итоговой матрице C = A + B элементы
, то в итоговой матрице C = A + B элементы  , с вычитанием все то же самое, только разность a и b. На практике это выглядит как сумма (или разность) соответствующих чиселУмножение матриц на некоторую константу. Если умножать матрицу A с элементами
, с вычитанием все то же самое, только разность a и b. На практике это выглядит как сумма (или разность) соответствующих чиселУмножение матриц на некоторую константу. Если умножать матрицу A с элементами  на некоторое постоянное число C, то C*A =
на некоторое постоянное число C, то C*A = 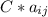 , т.е. умножаете это число на каждый элемент матрицы.
, т.е. умножаете это число на каждый элемент матрицы.Теперь давайте найдем по условию 3A
![3A = \left[\begin{array}{cc}12&-3\\9&6\end{array}\right]](/tpl/images/0988/6779/046d9.png)
Теперь 2B:
![2B = \left[\begin{array}{cc}-4&2\\10&6\end{array}\right]](/tpl/images/0988/6779/f0fc3.png)
Теперь поэлементно из одного вычитаем другое:
![C = 3A - 2B = \left[\begin{array}{cc}16&-5\\-1&0\end{array}\right]](/tpl/images/0988/6779/e2957.png)
1.
2.
3.
4.
если будут вопросы - задавайте
отметьте, , как лучший ответ, если не сложно ❤️
на киви не надо, если что
Обозначим за v - скорость работы первой бригады, u- скорость работы второй бригады. По условию задачи всю работу они могут выполнить за 30 дней, если работают вместе.
Пусть A - вся работа.
30*(u+v)=A (1)
Но на самом деле получилось по-другому. Сначала они работали 6 дней 6*(u+v), а потом дорабатывала вторая бригада 40 дней - 40u. То есть 6*(u+v)+40u. Опять таки вся работа была выполнена.
6*(u+v)+40u=А (2)
Приравняем левые части уравнений (1) и (2)
30*(u+v)=6*(u+v)+40u
30*(u+v)-6*(u+v)=40u
24(u+v)=40u
Делим обе части на 8.
3(u+v)=5u
3u+3v=5u
3v=5u-3u
3v=2u (3)
Выразим v через u
v=2/3u
Подставим в первое уравнение
30*(u+2/3u)=A
30*(5/3u)=A
30*5/3*u=A
50u=A
Здесь u - скорость выполнения работы второй бригадой. А - вся работа. Значит 50 суток - время, за которое выполнит всю работу вторая бригада одна.
Теперь выразим из 3-его уравнения u через v.
u=1,5v
Снова подставляем значение u через v в первое уравнение.
30*(1,5v+v)=A
30*2,5v=A
75v=A
Здесь v - скорость выполнения работы первой бригадой. А - вся работа. Значит 75 суток - время, за которое выполнит всю работу первая бригада одна.
ответ: 75 суток - время, за которое выполнит всю работу первая бригада одна.
50 суток - время, за которое выполнит всю работу вторая бригада одна.