Если прямая проходит через точку, то её координаты удовлетворяют уравнению прямой.
Другими словами, если подставить координаты точки, через которую проходит прямая, в уравнение прямой, мы получим верное равенство.
2х-у=4
А (0; 4)
х=0, у=4
2*0-4 = -4
-4 ≠ 4
Равенство неверное.
Вывод: прямая 2х-у=4 не проходит через точку А (0; 4).
В (2; 0)
х=2, у=0
2*2-0 = 4
4=4 (равенство верно)
Вывод: прямая 2х-у=4 не проходит через точку В (2; 0).
С (-3; -10)
х= -3, у= -10
2*(-3)-(-10) = -6+10 = 4
4=4 (равенство верно)
Вывод: прямая 2х-у=4 не проходит через точку С (-3; -10).
ответ: прямая проходит через точки В и С.
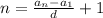
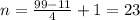
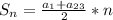
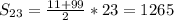
используя формулу разности квадратов: