Ядро в алгебре — характеристика отображения f:A– B ,обозначаемая ker f отражающая отличие f от инъективного отображения, обычно — множество прообразов некоторого фиксированного (нулевого, единичного, нейтрального) элемента e. Конкретное определение может различаться, однако для инъективного отображения f множество ker f всегда должно быть тривиально, то есть состоять из одного элемента (как правило, нейтрального элемента из A.
Если множества A и B обладают некоторой структурой (например, являются группами или векторными пространствами), то ker f также должно обладать этой структурой, при этом различные формулировки основной теоремы о гомоморфизме связывают образ Im f и фактормножество A/ker f
Правильно я условия записал?
1)
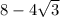= мы 4 выносим за скобки получится:
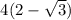= дальше мы 4 представляем как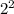 
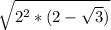= корень всё это время был и есть над этими числами просто ДО этого я типо его не писал, чтобы проще было смотреть. Теперь 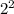это 4, корень из 4 = 2.
Вот и получается: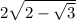 
2) 
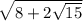использую формулу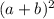 
получаем: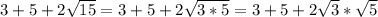 
дальше расставляем это так: 
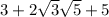и получаем формулу:
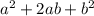сводим уравнение получается: 
.
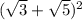Теперь не забываем, что у нас есть корень ещё один, который мы убрали, на время и получаем: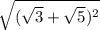 
, квадрат корней сокращается и получается: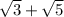 
а) а11=а1+10d = 5+10*1,2 = 17
б) а15 =а1+14d= -12+19,6 = 7,6
Объяснение: