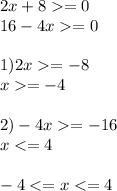
1) x^2+3x=0
x(x+3)=0
x=0 или x+3=0
x=-3
2)4x^2-12x=0
4x(x-3)=0
4x=0 или x-3=0
x=0 x=3
3)6x^2+2x=0
2x(3x+1)=0
2x=0 или 3x+1=0
x=0 x=-1/3
4)5x^2-x=0
x(5x-1)=0
x=0 или 5x-1=0
x+1/5
5)5x^2+2x=0
x(5x+2)=0
x=0 или 5x+2=0
x=-2/5
6)x^2-16=0
(x-4)(x+4)=0
x-4=0 или x+4=0
x=4 x=-4
7)2x^2-18+0
x^2=9
x=+-3
8)5x^2+20=0
x^2=-4
Решений нет!
9)16x^2-25=0
(4x-5)(4x+5)=0
4x-5=0 или 4x+5=0
x=5/4 x=-5/4
10)12x^2-6=0
x^2=0,5
А вот в этом уравнении получается бесконечная дробь! 0,707 Поэтому перепроверьте его!
правильного двенадцатиуголника
количество сторон тоже 12
каждая сторона - это основание равнобедренного треугольника с вершиной в центре
правильного двенадцатиуголника
величина угла при вершине 360/12=30
углы при основании (180-30) /2 =75
пусть боковая сторона каждого треугольника -b
тогда по теореме косинусов
a^2 = b^2 +b^2 -2*bb*cos30
a^2 = 2b^2(1-cos30) =2b^2(1-√3/2)=b^2(2-√3)
b^2 =a^2 / (2-√3)
площадь одного треугольника
S1 =1/2*b^2*sin30 =b^2/4 <---подставим b^2
S1 =a^2 / 4(2-√3) <---домножим числ. и знамен. на (2+√3)
S1 =a^2(2+√3) / 4(2-√3)(2+√3) =a^2(2+√3) / 4(4-3) =a^2(2+√3) / 4
общая площадь S= 12*S1 =12*a^2(2+√3) / 4 = 3a² (2+√3).
ДОКАЗАНО