1 шаг. Проверим справедливость утверждения при n=1:
- верно
2 шаг. Предположим, что при n=k следующее утверждение верно:
3 шаг. Докажем, что при n=k+1 следующее утверждение также будет верно:
Для доказательства выполним преобразования:
Рассмотрим получавшуюся сумму. Первое слагаемое делится на 9 по предположению, сделанному на предыдущем шаге. Во втором слагаемом первый множитель делится на 3. Значит, остается доказать, что второй множитель также делится на 3. Докажем это, используя арифметику остатков:
Мы получили, что выражение дает при делении на 3 такой остаток, как и число 3. Но число 3 кратно 3, значит и выражение кратно 3.
Возвращаясь к выражению , повторим, что первое слагаемое делится на 9, второе слагаемое представляет собой произведение двух множителей, каждое из которых делится на 3, то есть само слагаемое делится на 9. Сумма двух выражений, делящихся на 9, также делится на 9, или другими словами, кратна 9. Доказано.
Пусть х мест было в каждом ряду, тогда количество рядов было 320/х . После того, как зрительный зал увеличили мест стало (х+4) , а рядов 320 / х + 1 Составляем уравнение по условию задачи: (х+4) * ( 320/х + 1) = 420 х *320/x+4*320/x+x+4=420 320+1280/x+x+4=420 (умножим на x) 320x+1280+x²+4x=420x 324х+х²+1280-420х=0 х²-96 х +1280 = 0 D= b2-4ac=9216 - 4*1280 = 9216 -5120=4096 х1=(96+64) / 2 =80 х2 =(96-64) / 2 =16 320/16 + 1 = 21 ряд или 320/80+1=5 ряда (т.е. два варианта ответа: 21 ряд по 20 мест или 5 рядов по 84 места). ответ: 21 ряд (5 рядов).
Имеется такое простое решение: начнём с конца — после установки +4 мест в каждом ряду и добавлении +1 ряда посадочных мест стало 420, математически: Х*Y=420 - имеем одно уравнение. Тогда “до реконструкции” было X-4 мест в каждом ряду и Y-1 рядов, формулой: (X-4)*(Y-1)=320 - имеем систему уравнений, решая которую, получаем X1=20; Y1=21; X2=84; Y2=5. Странноватый расклад с 5-ю рядами по 84 места можно оставить в качестве диковинки, логичнее предпочесть вариант: стало 21 ряд по 20 мест в каждом.
1 шаг. Проверим справедливость утверждения при n=1:
2 шаг. Предположим, что при n=k следующее утверждение верно:
3 шаг. Докажем, что при n=k+1 следующее утверждение также будет верно:
Для доказательства выполним преобразования:
Рассмотрим получавшуюся сумму. Первое слагаемое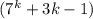 делится на 9 по предположению, сделанному на предыдущем шаге. Во втором слагаемом
делится на 9 по предположению, сделанному на предыдущем шаге. Во втором слагаемом 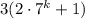 первый множитель делится на 3. Значит, остается доказать, что второй множитель также делится на 3. Докажем это, используя арифметику остатков:
первый множитель делится на 3. Значит, остается доказать, что второй множитель также делится на 3. Докажем это, используя арифметику остатков:
Мы получили, что выражение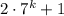 дает при делении на 3 такой остаток, как и число 3. Но число 3 кратно 3, значит и выражение
дает при делении на 3 такой остаток, как и число 3. Но число 3 кратно 3, значит и выражение 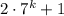 кратно 3.
кратно 3.
Возвращаясь к выражению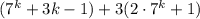 , повторим, что первое слагаемое делится на 9, второе слагаемое представляет собой произведение двух множителей, каждое из которых делится на 3, то есть само слагаемое делится на 9. Сумма двух выражений, делящихся на 9, также делится на 9, или другими словами, кратна 9. Доказано.
, повторим, что первое слагаемое делится на 9, второе слагаемое представляет собой произведение двух множителей, каждое из которых делится на 3, то есть само слагаемое делится на 9. Сумма двух выражений, делящихся на 9, также делится на 9, или другими словами, кратна 9. Доказано.