1)x-x/9=8/3
x*27-3(x/9)=9(8/3)
27(27x-3x)=72*27
729x-81x=1944
648x=1944
x=3
2)x-x/7=-9/14.
x*14-2(x/7)=-9/14
14(14x-2x)=-9*14
196x-28x=-126
168x=-126
x=-0.75
:)
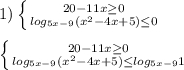
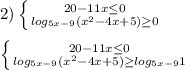
1.
216х² - 6у⁴ = 6 * (36х² - у⁴) = 6*(6х - у²)(6х + у²) (ответ Е),
2.
а)
S = 6а² = 6*(3х - 4)² = 6*(9х² - 24х + 16) = 54х² - 144х + 96,
б)
V = а³ = (3х - 4)³ = 27х³ - 108х² + 144х - 16,
3.
а)
4,3² - 2,58 + 0,3² = 4,3² - 2*4,3*0,3 + 0,3² = (4,3 - 0,3)² = 4² = 16,
б)
(44² - 12²) / (56² - 16²) = (44 - 12)(44 + 12) / (56 - 16)(56 + 16) =
= (32*56) / (40*72) = 28/45,
4.
1 число - х,
2 число - (х-52),
х² - (х-52)² = 208,
х² - х² + 104х - 2704 = 208,
104х = 208 + 2704,
104х = 2912,
х = 28 - 1 число,
х-52 = 28 - 52 = -24 - 2 число
1)9x/9-x/9=8/3
8x/9=8/3
8x=24
x=3))
7x/7-x/7=-9/14
6x/7=-9/14
6x=7(-9)/14
6x=-4.5
x=-0.75