Вот <3
Объяснение:
3x - 5y = 13
Решаем в общем виде.
y = (3x - 13)/5 = (-10 + 3x - 3)/5 = -2 + 3(x - 1)/5
Чтобы оба числа были целыми, разность x - 1 должна делиться на 5.
Или наоборот
x = (5y + 13)/3 = (3y + 12 + 2y + 1)/3 = y + 4 + (2y + 1)/3
Чтобы оба числа были целыми, сумма 2y + 1 должна делиться на 3.
Например, подходит решение:
x = 1, y = -2: 3*1 - 5(-2) = 3 + 10 = 13
Или x = 6, y = 1: 3*6 - 5*1 = 18 - 5 = 13
Или x = 11, y = 4: 3*11 - 5*4 = 33 - 20 = 13
Достаточно найти одну пару целых решений, из нее получаются другие решения. Для этого надо прибавлять 5 к x и прибавлять 3 к y.
Периметр — это сумма длинн всех сторон.
Нужно найти длины векторов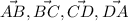
.
Длина вектора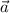
обозначается как 
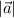и вычисляется по формуле
Координаты вектора AB находятся по формуле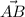
= {
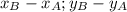}, когда 
.
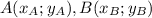Вот и все формулы. Находим координаты четырёх векторов, находим длины этих векторов, складываем и находим тем самым периметр четырёхугольника ABCD.
Итак, A(-3; -2), B(2; 5), C(5; 2), D(0; -5).