Объяснение:
Линейное уравнение – уравнение, сводящееся к виду ax+b=0, где a≠0,b – числа. Линейное уравнение всегда имеет единственное решение x=−ba. Квадратное уравнение – уравнение, сводящееся к виду ax2+bx+c=0, где a≠0,b,c – числа. Выражение D=b2−4ac называется дискриминантом квадратного уравнения. Квадратное уравнение может иметь не более двух корней: ∙ если D>0, то оно имеет два различных корня и x1=−b+D2aиx2=−b−D2a ∙ если D=0, то оно имеет один корень (иногда говорят, что два совпадающих) x1=x2=−b2a ∙ если D<0, то оно не имеет корней. ▸ Теорема Виета для квадратного уравнения: Если квадратное уравнение имеет неотрицательный дискриминант, то сумма корней уравнения x1+x2=−ba а произведение x1⋅x2=ca ▸ Если квадратное уравнение: ∼ имеет два корня x1 и x2, то ax2+bx+c=a(x−x1)(x−x2). ∼ имеет один корень x1 (иногда говорят, что два совпадающих), то ax2+bx+c=a(x−x1)2. ∼ не имеет корней, то квадратный трехчлен ax2+bc+c никогда не может быть равен нулю. Более того, он при всех x строго одного знака: либо положителен, либо отрицателен. ▸ Полезные формулы сокращенного умножения: x2−y2=(x−y)(x+y)(x+y)2=x2+2xy+y2(x−y)2=x2−2xy+y2 Ознакомиться с полной теорией
Объяснение:
Координаты точки пересечения можно найти методом вычитания:
а)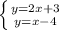 
чтобы найти переменную 
, достаточно вычесть от верхней части системы нижнюю, тогда получится 
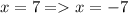, найдем координату 
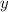, подставим значение х в любую часть системы: 
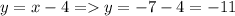, следовательно точка пересечения этих прямых будет находится по координатам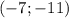 
б)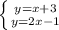 
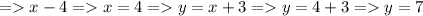, искомый ответ будет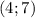 
в)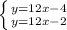 
тут возникает противоречие, если прямые вычесть, то мы не сможем найти или 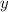, или же будет 
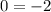, что не является верным, значит прямые не будут пересекаться, они являются параллельными
г)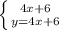 
тут уже можно сразу найти 
, искомый ответ будет 
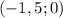
ответ: а)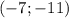, б)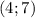, в)Нет решения, г)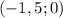
Примечание: Если в г была система такая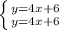 
, то это это две прямые, которые совпадают и ответом будет бесконечное множество.
По трём точкам А, В и С составим уравнение плоскости.
Для составления уравнения плоскости используем формулу:
x - xA y - yA z - zA
xB - xA yB - yA zB - zA
xC - xA yC - yA zC - zA = 0
Подставим данные и упростим выражение:
x - 1 y - 2 z - (-1)
0 - 1 1 - 2 5 - (-1)
(-1) - 1 2 - 2 1 - (-1) = 0
x - 1 y - 2 z - (-1)
-1 -1 6
-2 0 2 = 0
(x - 1) (-1·2-6·0) - (y - 2) ( (-1)·2-6·(-2)) + (z - (-1)) ((-1)·0-(-1)·(-2)) = 0
(-2) (x - 1) + (-10) (y - 2) + (-2)(z - (-1)) = 0
- 2x - 10y - 2z + 20 = 0 или, сократив на (-2):
x + 5y + z - 10 = 0.
Теперь подставим в полученное уравнение координаты точки Д.
Если уравнение превратится в тождество - то точка принадлежит плоскости вместе с точкам А. В и С.
Д(2;1;3)
2 + 5*1 + 3 - 10 = 0.
0=0.
ответ: точка Д принадлежит плоскости.