Пусть х - время, за которое Иван может вспахать все поле.
Тогда х+5 - время, за которое все поле может вспахать Григорий.
Примем всю площадь поля за 1.
Тогда 1/х - производительность Ивана.
1/(х+5) - производительность Григория.
1/х + 1/(х+5) - производительность Ивана и Григория, работающих вместе что соответствует 1/6.
Уравнение
1/х + 1/(х+5) = 1/6
Умножим обе части неравенства на 6х(х+5), чтобы избавиться от знаменателей.
6х(х+5)/х + 6х(х+5)/(х+5) = 6х(х+5)/6
6(х+5) + 6х = х(х+5)
6х+30 + 6х = + х^2 + 5х
х^2 - 7х - 30 = 0
D = 49 -4(-30) = 49 + 120 = 169
√D = √169 = 13
x1 = (7-13)/2 = -6/2 = -3 - не походит, поскольку время не может отрицательным.
х2 = (7+13)/2 = 20/2 = 10 часов - время, за которое Иван вспашет все поле.
ответ: 10 часов
Проверка
1) 1:10= 1/10 - производительность Ивана.
2) 1:6 = 1/6 - производительность Ивана и Григория, работающих вместе.
3) 1/6 - 1/10 = 5/30 - 3/30 = 2/30 = 1/15 - производительность Григория.
4/ 1 : 1/15 = 15 часов- за такое время Григория может выполнить всю работу.
5) 15-10=5 часов - на столько часов Иван выполнит работу раньше, чем Григорий.
Подробнее - на -
Объяснение:
А) т.к. события независимые, то вероятность того, что мишень будет поражена дважды равна произведению вероятностей А и В
P(ав) = p(а) * p(в) = 0,9 * 0,3 = 0,27
Б) вер-сть того, что 1-ый не попадет : 1-0,9=0,1
вер-сть того, что 2-ой не попадет : 1-0,3 = 0,7
р(а) * р(в) = 0,1 * 0,7 = 0,07
В) т.к. наступит либо событие А, либо событие В, то речь идет о сумме событий А и В.
р(а+в) = р(а) + р(в) - р(а*в) = 0,9 + 0,3 - 0,27 = 0,93
Г) будет поражена ровно 1 раз в том случае, если произошло событие р(а+в) и не произошло р(ав)
р = 0,93-0,27=0,66
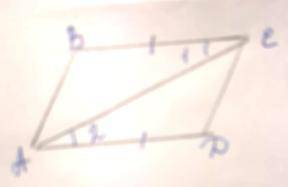
2. угол 1=2 (по условию)
3. ac- общая сторона
4. из пунктов 1-3 следует, что adc=abc по первому признаку равенства треугольников
теорема доказана
если dc=bc, значит
угол adc=abc=108
dca = acb = 32