Для начала вспомним графики функций y = [x] и y = {x}:
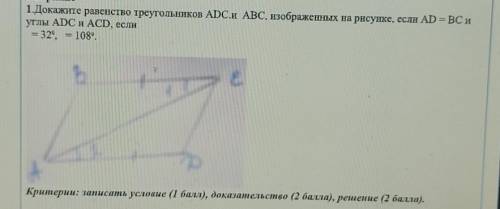
Первый представляет собой целую часть числа x. Например
[3,2] = [3 + 0,2] = 3
[-4,5] = [-5 + 0,5] = -5
График такой функции прикреплён во вложении.
Второй представляет собой дробную часть аргумента x, то есть y = x - [x]. Например
{3,2} = 3,2 - 3 = 0,2
{-4,5} = -4,5 - (-5) = 0,5
График также во вложении.
Теперь перейдём к заданию:
При выполнении используются правила геометрических преобразований.
1) y = [x + 1]
Берём за основу график функции y = [x] и смещаем его влево вдоль оси OX на 1.
2) y = [x] + 2
Берём за основу график функции y = [x] и смещаем его вверх вдоль оси OY на 2 единицы.
3) y = {x - 1/3}
Берём за основу график функции y = {x} и смещаем его вправо вдоль оси OX на 1/3 единицы.
4) y = {x} + 1
Берём за основу график функции y = {x} и смещаем его вверх вдоль оси OY на 1.
5) y = [3x + 1]
Сначала рассмотрим график y = [x + 1]. Он уже построен в пункте 1)Но в требуемом графике "3x", поэтому нужно к графиком y = [x + 1] применить ещё одно преобразование:Сначала рассмотрим график y = [3x]. По правилу геометрического преобразования, чтобы построить этот график, надо график функции y = [x] сжать в 3 раза вдоль оси OX.Так как в нашем случае функции имеет вид y = [x + 1], то и сжимать в три раза будем именно её.Таким образом, чтобы построить график функции y = [3x + 1] надо:
1) Взять за основу график функции y = [x] и сместить его влево вдоль оси OX на 1.
2) Полученный график сжать вдоль оси OX в 3 раза.
Все графики во вложении
![Построить график функции: 1) у=[х+1]; 2) у=[х]+2; 3) у={х-1/3}; 4) у={х}+1; 5) у=[3х+1]. с объяснени](/tpl/images/0968/4679/f1000.jpg)
![Построить график функции: 1) у=[х+1]; 2) у=[х]+2; 3) у={х-1/3}; 4) у={х}+1; 5) у=[3х+1]. с объяснени](/tpl/images/0968/4679/62280.jpg)
D = a^2 + 4a + 4
Уравнение не имеет действительных корней, если D < 0
a^2 + 4a + 4 < 0
(a + 2)^2 < 0
Ну таких значений a нет.
Хмм. Вроде не ошибся.
Еще можно так
х^2 - ax - a - 1=0
x^2 - 1 - a(x + 1) = 0
(x - 1)(x + 1) - a(x + 1) = 0
(x + 1)(x - 1 - a) = 0
x = -1
x = 1 + a
Один из корней зависит от параметра а. В таком случае, если не ошибаюсь, каким бы ни был параметр, один из корней всегда будет от него зависеть. Наш дискриминант получился равным (a + 2)^2. При a = -2 мы получаем 1 корень, или, если выражаться точнее, два одинаковых корня, что мы и получаем, подставив -2 в уравнение
x = 1 + a
Поэтому тут всегда есть корни