10 (км/час) - скорость велосипедиста.
Объяснение:
Из пункта А в пункт В, расстояние между которыми 20 км, одновременно выехали автомобилист и велосипедист. Известно, что скорость автомобилиста на 90 км/ч больше, чем скорость велосипедиста. Определите скорость (в км/ч) велосипедиста, если известно, что он прибыл в пункт В на 1 часов 48 минуты позже, чем автомобилист?
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - скорость велосипедиста.
х+90 - скорость автомобилиста.
20/х - время велосипедиста.
20/(х+90) - время автомобилиста.
Разница во времени 1 час 48 минут=1 и 4/5 часа=9/5 часа, уравнение:
20/х - 20/(х+90)=9/5
Общий знаменатель 5х(х+90), надписываем над числителями дополнительные множители, избавляемся от дроби:
20*5(х+90) - 20*5х=9*х(х+90)
100х+9000-100х=9х²+810х
-9х²-810х+9000=0/-1
9х²+810х-9000=0
Разделить уравнение на 9 для упрощения:
х²+90х-1000=0, квадратное уравнение, ищем корни:
D=b²-4ac =8100+4000=12100 √D= 110
х₁=(-b-√D)/2a
х₁=(-90-110)/2= -200/2= -100, отбрасываем, как отрицательный.
х₂=(-b+√D)/2a
х₂=(-90+110)/2
х₂=20/2
х₂=10 (км/час) - скорость велосипедиста.
10+90=100 (км/час) - скорость автомобилиста.
Проверка:
20/10=2 (часа) - время велосипедиста.
20/100=0,2 (часа)=12 минут - время автомобилиста.
Разница: 2(часа)-12(минут)=1(час)48(минут), верно.
Это произведение оканчивается 18-ю нулями.
Объяснение:
Как лучше записать вычисления- смотри в конце, а пока я объясню их смысл на словах.
Дело в том, что ноль в конце произведения простых множителей может дать только пара из множителей 2 * 5 (= 10). И сколько этих пар будет- столько и нулей в конце произведения.
Поэтому, количество нулей в конце произведения можно найти и не вычисляя полностью само произведение, а следуя по такому алгоритму:
1) разложить каждый множитель произведения на простые множители
2) если нужно- упростить полученное выражение (каждый простой множитель должен быть записан один раз, в виде степени с соответствующим показателем
3) у простых множителей 2 и 5 смотрим их показатели степеней - меньшее из этих двух чисел и будет равно количеству нулей, на которое будет оканчиваться всё произведение
4) если нет хотя бы одного из этих множителей- двойки или пятёрки или обоих вместе- значит не будет и нулей в конце произведения (можно считать, что показатель степени отсутствующего множителя равен нулю, а значит (смотри пункт 3) не будет и нулей в конце произведения)
Нахождение количества нулей в конце произведения лучше всего записать виде вот такого преобразования (может быть это даже понятнее, чем выше описанный алгоритм):
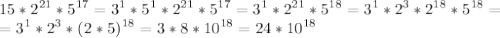
На этом преобразования можно закончить, само произведение думаю писать не обязательно в виде единого числа, т.к. количество нулей в его конце ясно видно в показателе степени десятки.
Ну если уж хочется, то можно и написать его в конце преобразований:
= 24 000 000 000 000 000 000
Я так понимаю функция y=11^(6x-x^2).
Так как в основании степени число 11, а оно больше единицы, то максимума функция будет достигать при наибольшем значении степени.
Рассмотрим функцию y=6x-x^2 - квадратичная функция, график парабола, ветви направлены вниз. Значит, наибольшего значения будет достигать в вершине параболы. Найдем абсциссу вершины: x=-b/2a=-6/-2=3. Значит в точке x=3 функция y=6x-x^2 достигает максимума, а, значит, и функция y=11^(6x-x^2) будет достигать максимума в точке x=3