Площади двух частей фигуры: 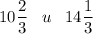
Объяснение:
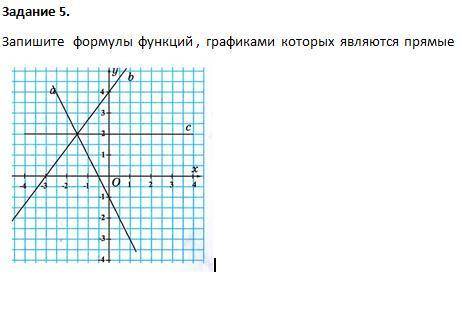
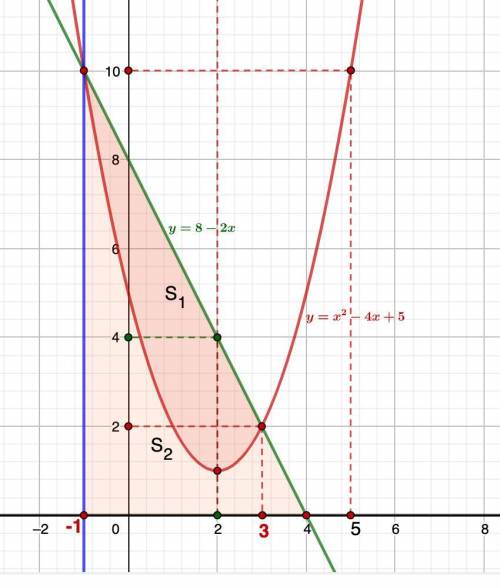
Требуется построить фигуру, ограниченную линиями y=8-2x, y=0, x=-1. График функции y = x^2-4x+5 делит фигуру на две части, найти площадь каждой части.
Построим графики данных функций и определим фигуру, ограниченную этими графиками.
1. у = 0
Это ось 0х.
2. х = -1
- прямая, проходящая через точку х = -1 и параллельная оси 0у.
3. у = 8 - 2х
- линейная функция, график прямая.
Для построения достаточно двух точек.
х = 2; у = 4
х = -1; у = 10
Получили треугольник, ограниченный тремя линиями.
4. у = х² - 4х + 5
- квадратичная функция, график парабола, ветви вверх.
Вершина:
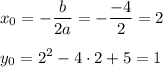
х₀ = 2 - ось симметрии.
Возьмем еще две точки:
х = 3; у = 2;
х = 5; у = 10
Вторую ветвь построим симметрично прямой х = 2.
5. Найдем точки пересечения графиков у = х² - 4х + 5 и у = 8 - 2х:
х² - 4х + 5 = 8 - 2х
х² - 2х -3 = 0
По теореме Виета:
х₁ = -1; х₂ = 3
6. Парабола делит треугольник на две части, площади которых S₁ и S₂.
Найдем площадь треугольника S.
Один катет равен:
4 - (-1) = 5
Другой катет равен 10.
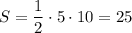 (ед.²)
(ед.²)
7. Найдем площадь S₁ по формуле:
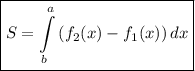
Имеем:
a = 3; b = -1; f₂(x) = 8 - 2x; f₁(x) = x² - 4x + 5
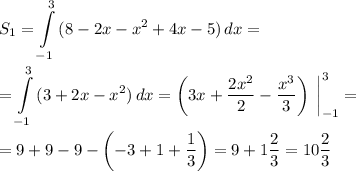 (ед.²)
(ед.²)
8. Найдем площадь S₂:
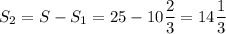 (ед.²)
(ед.²)
Площади частей фигуры 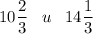
1) В точке х₀=2, у= -1 - уравнение касательной
2) 6 с
Объяснение:
1) Касательная к графику функции f(x) =3x² -12х +11 будет параллельна оси абсцисс в точке, в которой производная к данной функции равна нулю, т.е. в точке х₀, где f `(x₀)=0. Найдем эту точку:
f(x) =3x² -12х +11
f `(x)=3*2x-12 = 6x-12
f `(x₀) =0 при 6x₀-12=0
6x₀=12
x₀=2 - искомая точка
y = y(x₀) + y `(x₀)(x-x₀)
y = (3*2²-12*2+11)+0*(x-2)
y=(3*4-24+11)+0
y = -1 - уравнение касательной в точке х₀=2
2) x(t) = 2,5t²-10t+11
v(t) = x`(t)
v(t) = (2,5t²-10t+11)`=2,5*2t-10+0 = 5t-10
v(t) = 20 (м/с)
5t-10 = 20
5t = 30
t = 6 (c) - искомое время