
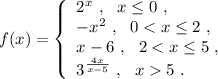
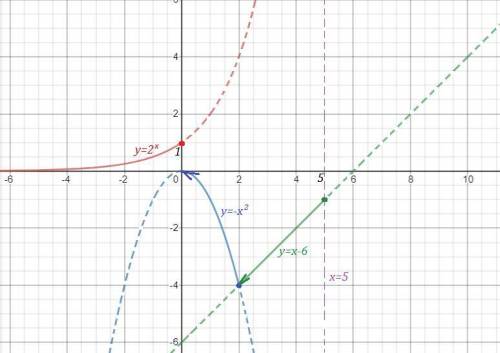
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
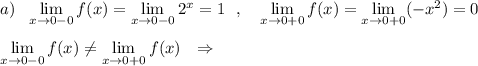
При х=0 функция имеет разрыв 1 рода .
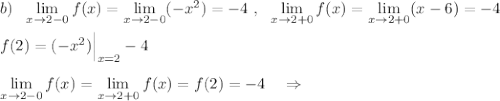
При х=2 функция непрерывна.
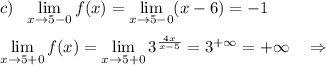
При х=5 функция имеет разрыв 2 рода .
График функции нарисован сплошной линией.
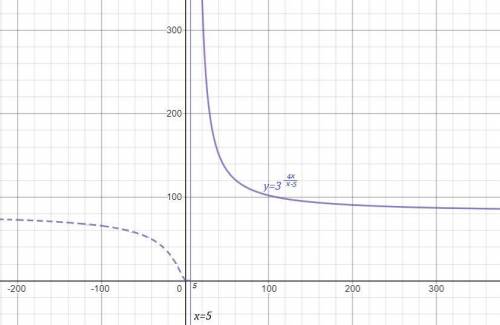
На 1 рисунке нет чертежа функции 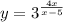 при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
1.(-1,5+4-2,5)(-6)
-1.5+4=2.5
2.5-2.5=0
В первой скобке будет 0.
0 нельзя умножать на другое число, следовательно
ответ:0
2.
Скобка первая: (0,2-0,25)=-0,05
Решим вторую скобку: -1,6-3,3=-4,9
-4,9+5=0,1
Делим первую на вторую: -0,05:0,1=-0,5
ответ: -0,5
Задание №2.
1. 2(х-1)=3(2х-1)
Первая скобка: умножаем 2 на каждый множитель и получается: 2х-2=
Тоже самое и со второй скобкой: 6х-1
Получается: 2х-2=6х-1
Все числа с "х" переносим в правую сторону, а обычные числа в левую. Получается:
2х-6х=2-1(Главное помнить,что при переносе числа через знак "равно" знак числа меняется на противоположный.)
Решаем уравнение:
2х-6х=2-1
-4х=1
х=
х=-0,25
ответ: -0,25
2. 3-5(х-1)=х-2
Раскрываем скобки: 3-5х+1=х-2
"х" переносим в права, а обычные числа в лево:
-5х-х=-3-1-2
-6х=-6
х=6
ответ: 6
4.
приравняем обе части к общему знаменателю( у 3 и 2 это 6):
с "х" перенесем в права, обычные числа в лево:
умножим крест - на - крест. получим:
0,5*6=-х*1
3=-х
х=-3
ответ: -3