Известно, что 2a²b³ = 6. Найдите значение выражения: 1) –6a²b³; 2) 2а⁴b^6

Question

Алгебра: Известно, что 2a²b³ = 6. Найдите значение выражения: 1) –6a²b³; 2) 2а⁴b^6​

AgentRuba · Accepted Answer

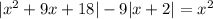
|x^2+9x+18|-9|x+2|=x^2

Подмодульные выражения обращаются в нуль

1)

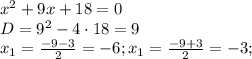
$x^2+9x+18=0\\D=9^2-4\cdot 18=9\\x_{1}=\frac{-9-3}{2}=-6; x_{1}=\frac{-9+3}{2}=-3;$

2)

$x+2=0\\x=-2$

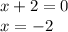
Эти точки разбивают числовую прямую на 4 промежутка

Раскрываем знак модуля на каждом из промежутков

(-∞;-6]

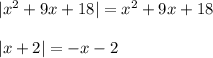
|x^2+9x+18|=x^2+9x+18|x+2|=-x-2

Уравнение принимает вид:

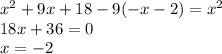
$x^2+9x+18-9(-x-2)=x^2\\18x+36=0\\x=-2$

не принадлежит рассматриваемому промежутку, значит уравнение не имеет корней на (-∞;-6)

(-6;-3]

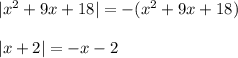
|x^2+9x+18|=-(x^2+9x+18)|x+2|=-x-2

Уравнение принимает вид:

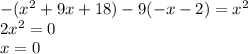
$-(x^2+9x+18)-9(-x-2)=x^2\\2x^2=0\\x=0$

не принадлежит рассматриваемому промежутку, значит уравнение не имеет корней на (-6;-3)

(-3;-2]

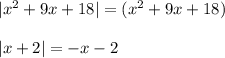
|x^2+9x+18|=(x^2+9x+18)|x+2|=-x-2

Уравнение принимает вид:

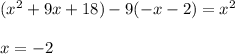
(x^2+9x+18)-9(-x-2)=x^2x=-2

принадлежит рассматриваемому промежутку(-3;-2] , значит уравнение имеет корень х=-2

(2;+∞)

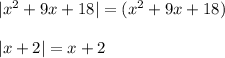
|x^2+9x+18|=(x^2+9x+18)|x+2|=x+2

Уравнение принимает вид:

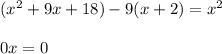
(x^2+9x+18)-9(x+2)=x^20x=0

уравнение верно при любых x∈(2;+∞)

О т в е т. {2} U (2;+∞) =[2;+∞)

Известно, что 2a²b³ = 6. Найдите значение выражения: 1) –6a²b³; 2) 2а⁴b^6​