y1= 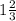 ; y2= 1
; y2= 1
Объяснение:
a=3; b=-8; с=5
D= b²-4ac= (-8)²-4×3×5= 64-60=4=2²
y=-b±√D = 8±2
2a 6
y=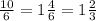
y=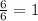
 , где A, B, C - координаты нормального вектора плоскости N(A,B,C).
, где A, B, C - координаты нормального вектора плоскости N(A,B,C). ⇒ N(2,-3,4).
⇒ N(2,-3,4). , где
, где 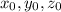 - координаты точки M(
- координаты точки M(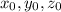 ), через которую проходит прямая,
), через которую проходит прямая,  - координаты направляющего вектора S(
- координаты направляющего вектора S( ).
). ) = N(A,B,C) ⇒ N(2,-3,4) = S(2,-3,4); M(1,-2,3).
) = N(A,B,C) ⇒ N(2,-3,4) = S(2,-3,4); M(1,-2,3).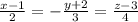
3y²-8y+5=0.
a=3, b=-8, c=5.
По-методу коэффициентов, если a+b+c=0, то корни x1=1, x2=c/a.
a+b+c=3+(-8)+5=-5+5=0.
x1=1, x2=5/3 = 1⅔.