Т.к. площадь (S) прямоугольного треугольника равна 42см^2, то
ab/2=S
где a и b катеты этого треугольника.
Т.к. сумма катетов равна 15,5 см, то
a+b=15,5
Составляем систему уравнений:
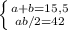
Выражаем из первого уравнения a:
a=15,5-b
Выражаем из второго уравнения a:
a=84/b
Подставляем и получаем:
15,5-b=84/b
Умножаем обе части уравнения на b и переносим все части этого уравнения в ghfde. часть:
b^2-15,5b+84=0
Находим дискрименант:
D=15,5^2-4*1*84=240,25-336<0
Дискрименант оказался отрицательным числом, следовательно уравнение нерешаемо, следовательно я доказал, что треугольник с такими соотношениями не существует!
P.S. 2 раза перепроверял.
Возьмём скорость пропускания второй трубы за х, тогда скорость пропускания первой=х-4
Время, за которое первая труба заполняет 672л воды=672/х-4, а время, за которое 2 труба заполняет 560л воды=560/х. Известно что 2 труба заполняет свой резервуар на 8 минут быстрее, поэтому можно составить уравнение:
672/(х-4) - 560/х=8 домножаем всё на х(х-4) сразу укажем что х не может быть равен 4 (тк при этом идёт деление на ноль чего делать нельзя)
получаем:
672х-560(х-4)=8х(х-4)
672х-560х+2240=8х^2-32х переносим всё в правую часть и считаем
8х^2-144х-2240=0 разделим всё на 8
х^2-18х-280=0
D=18*18+4*280=324+1120=38^2
отсюда х1=(18-38)/2=-10(пост корень тк скор пропускания не может быть отриц)
х2=18+38/2=28
Значит 1 труба пропускает 28-4=24л воды а вторая-28л воды