Примем за 1 объем бассейна. Время наполнения бассейна в часах: x - через обе трубы, x+16 - только через 1-ю трубу, x+25 - только через 2-ю трубу. Скорости наполнения: 1/x - через обе трубы, 1/(x+16) - только через 1-ю трубу, 1/(x+25) - только через 2-ю трубу. Значит, 1/(x+16)+1/(x+25)=1/x. Умножим обе части уравнения на x(x+16)(x+25): x(x+25)+x(x+16)=(x+16)(x+25), x^2+25x+x^2+16x=x^2+41x+400, 2x^2+41x=x^2+41x+400, x^2=400. Так как x>0, то x=20. Через обе трубы бассейн наполняется за 20 часов, только через 1-ю трубу - за 20+16=36 часов, только через 2-ю трубу - за 20+25=45 часов. Проверка: 1/36+1/45, 5/180+4/180=9/180=1/20. ответ: обе трубы наполняют бассейн за 20 часов.
1. а) значение аргумента равно 3, тогда значение функции:
б) Согласно условию значение функции равно 5, то есть,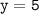
, то значение аргумента найдем, решив следующее уравнение:
в) Подставляя координаты точки В в график уравнения, получим
Раз выполняется тождество, следовательно, график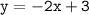
проходит через точку В(-1;5).
2. Графиком линейной функции является прямая. Для построения прямой достаточно взять две точки, например: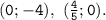
а) значению аргумента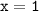
соответствует значение функции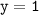 
б) значению функции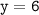
соответствует значение аргумента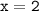 
3. Точки пересечения с осью координат Х. График функции пересекает ось Х при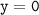
, значит нужно решить уравнение:
Точки пересечения с осью координат У. График пересекает ось У, когда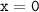
, то есть, подставляя х=0 в график уравнения, получим
4. Раз график функции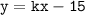
проходит через точку 
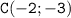, значит значение 
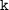найдем, подставив координаты точки C, имеем