
1. у=4х-2
1)
х=0 у=4*0-2=-2
х=6 у=4*6-2=10
2)
у=0
4х-2=0
4х=2
х=0,5
у=2
4х-2=2
4х=4
х=1
2.
Пересечение с осью ОХ:
у=0
1,2х-24=0
1,2х=24
х=20
(20; 0)
Пересечение с осью ОУ:
х=0
у=1,2*0-24
у=-24
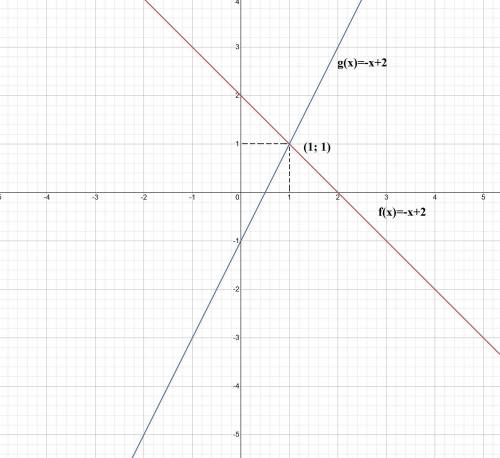
3. Поскольку оба графика линейные функции, то для построения достаточно 2х точек:
f(x)=-x+2
x y
0 2
1 1
g(x)=2x-1
x y
0 -1
2 3
1) Из графика видно, что точка пересечения (1; 1)
2) Из построенных графиков видно, что g(x)>f(x), при х>1.
4. График линейной функции имеет вид:
у=kx+b
a График проходит через точки (0; 0), (1; 1)
0=k*0+b ⇒b=0
1=k*1 ⇒k=1
у=х
б) Графиком является постоянная функция:
у=-2
в) График проходит через точки (0; 3) и (3;0)
3=0*k+b ⇒b=3
0=3k+b
3k=0-3
k=-1
y=-x+3
Ц*Ч=В
(Ц-Х)*(Ч+0,25*Ч)=В+0,125*В
где Ц - цена входного билета (изначально), Ч - число зрителей, В - выручка, Х - на сколько снизилась цена бета
Преобразуем систему:
Ц*Ч=В или Ч=В/Ц
(Ц-Х)*1,25*Ч=1,125*В
Подставим:
(Ц-Х)*1,25*В/Ц=1,125*В
Разделим обе части уравнения на В (т. к. В (выручка) на равна 0):
(Ц-Х)*1,25/Ц=1,125
Раскроем скобки:
1,25-1,25*Х/Ц=1,125
Подставим вместо Ц значение Ц = 20:
1,25-1,25*Х/20=1,125
1,25-0,0625*Х=1,125
1,25-0,0625*Х=1,125
0,125=0,0625*Х
Х=2
Новая цена, равная Ц-Х=20-2=18.