Объяснение:
1.
a) 3a*(3a+2b)-(a+b)²=9a²+6ab-a²-2ab-b²=8a²+4ab-b².
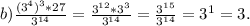
2.
6x-5*(2x+1)=5*(2-3x)
6x-10x-5=10-15x
11x=15 |÷11
x=15/11.
3.
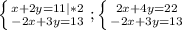
Суммируем эти уравнения:
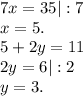
ответ: x=5 y-3.
4. a³-25a=a*(a²-5²)=a*(a+5)*(a-5).
5.
Пусть во второй пачке х книг. ⇒
(x+5)+x+(3*x)=45
x+5+x+3x=45
5x+5=45
5x=40 |÷5
x=8.
8+5=13
3*8=24
ответ: в первой пачке 13 книг, во второй пачке 8 книг,
в третьей пачке 24 книги.
6.
a) y=3x-4 y=3x+1
3x-4=3x-1 -4≠-1 ⇒ прямые не пересекаются.
б) y=4x-6 y=x+6
4x-6=x+6 3x=12 |÷3 x=4 ⇒ y=4+6 у=10.
Координаты точки пересечения: (4;10).
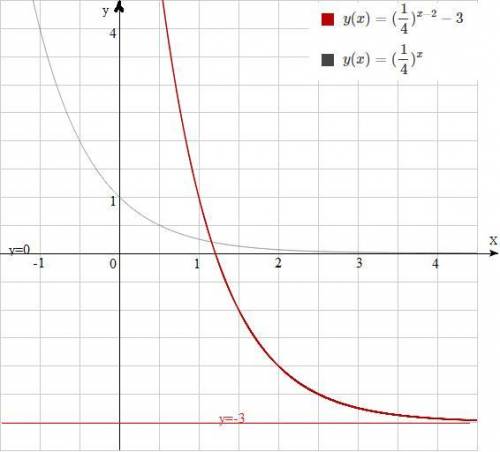
Решите и постройте график функции у=(1/4)ˣ⁻²-3
Объяснение:
у=(1/4)ˣ⁻²-3 можно построить сдвигом графика у=(1/4)ˣ на
- "2" по ох вправо ,
-"3" по оу вниз.
Функия у=(1/4)ˣ -убывающая, т.к. 0<1/4<1 .Построим таблицу значений для у=(1/4)ˣ и затем сдвинем каждую точку на указанные значения:
х...-1......0......1
у...4......1.....0,25.
Точка (-1;4) при данном сдвиге перейдет в (1;1),
Точка (0;1 ) при данном сдвиге перейдет в (2;-2 ),
Точка (1 ;0,25) при данном сдвиге перейдет в (3 ;-2,75),
Горизонтальная асимптота у=0 перейдет в у=-3.
а) Сколько имеется различных освещения коридора, включая случай когда все лампочки не горят. Как видим, каждая лампочка имеет два состояния (горит/не горит). Т.к. лампочек три, то всего вариантов будет 2³ = 8. Все 8 вариантов представлены на рисунке.
б) Сколько имеется различных освещения, если известно что лампочки №1 и №2 горят или не горят одновременно? Когда лампочки №1 и №2 горят, то лампочка №3 либо горит, либо не горит (2 варианта). Точно также, когда лампочки №1 и №2 не горят, то лампочка №3 тоже либо горит, либо не горит (2 варианта). Итого, 4 варианта. Проверяем по рисунку.
в) Сколько имеется различных освещения, если известно что при горящей лампочке №3 лампочка №2 не горит?
По рисунку считаем варианты - их 6. Когда лампочка №3 горит, то лампочка №2 не горит (по условию), а у лампочки №1 есть 2 варианта - горит/не горит. Когда лампочка №3 не горит, то вариантов у оставшихся лампочек будет 2² = 4. Вот и получается 6 вариантов.
г) сколько имеется различных освещения коридора когда горит большинство лампочек? Т.е. нам надо сосчитать случаи, когда одновременно горят 2 и более лампочек. По рисунку высчитываем, что есть 4 варианта. Или считаем число сочетаний двух лампочек из трёх, плюс число сочетаний три лампочки из трёх.
Итак, 4 варианта.