вспомним что такое модуль
|x| = x x>=0
= -x x<0
Пишем на всякий случай ОДЗ x≠3 и смотрим подмодульное выражение
(x²+x-2)/(x-3) = (x+2)(x-1)/(x-3)
D=1+8 = 9
x12=(-1+-3)/2 = -2 1
смотрим метод интервалов
[-2] [1] (3)
Итак при
1. x∈[-2 1) U (3 + ∞)
|(x²+x-2)/(x-3)| = (x²+x-2)/(x-3)
2. x∈(-∞-2) U [1 3)
|(x²+x-2)/(x-3)| = - (x²+x-2)/(x-3)
решаем полученные уравнения
1. x∈[-2 1] U (3 + ∞)
(x²+x-2)/(x-3) = (x²+x-2)/(x-3) решения все числа на интервалах с учетом одз
x∈[-2 1) U (3 + ∞)
2. x∈(-∞-2) U (1 3)
(x²+x-2)/(x-3) = - (x²+x-2)/(x-3)
2(x²+x-2)/(x-3) = 0
x=1 x=-2 решений нет
ответ x∈[-2 1] U (3 + ∞)
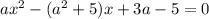
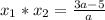
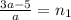, где n1 - нат. число. Тогда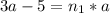
.
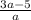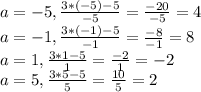
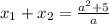
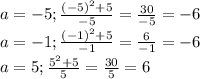
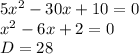
Объяснение:
x-5 не равно 0
x не равно 5