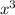-3
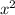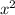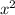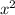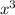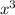
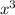А. y|=12-6x. Б. y|=3-6х В. y|=6-6. -6x.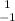
(x^2-x+3)dx
Объяснение:
Найдите наименьшее значение функции
у = 3х – 2
на промежутке (–1; 2]
это линейная ВОЗРАСТАЮЩАЯ функция. значит она может иметь максимум или минимум только НА КОНЦАХ области определения! Один конец открытый,-1 не принадлежит области,а вот второй закрытый! Х=2 граница области. У=3*2-2 У=4. Значит точка (2;4) и есть максимум данной функции на области определения.
Что насчет минимума? Можно как угодно ближе приближаться к -1 и получать все меньшие значения! Значит тут минимума не существет... последний ответ.
1) 10;
2) –2;
3) –10;
4) не существует.
2) приравниваем её к нулю и решаем получившееся уравнение
3) Смотрим: какие корни попали в указанный промежуток и ищем значения данной функции в этих точках и на концах данного отрезка;
4) пишем ответ.
Поехали?
1) f'(x) = ((x² -8x)'(x+1) - (x² -8x)(x+1)')/(x+1)²=
((2x-8)(x+1) - (x²-8x))/(x+1)²= (2x² -8x +2x -8 - x² +8x)/(x+1)²=
=(x² +2x -8) / (х+1)²
2)(x² +2x -8) / (х+1)² ⇒ x² +2x -8 =0, ⇒ х = - 4 и х = 2
3) Из найденных корней в указанный промежуток попало х = -4
а) х = -4
f(-4) = (-4)² -8*(-4) /(-4+1) = 48/(-2) = -24
б) х = -5
f(-5) = (-5)² -8*(-5) /(-5+1) = 65/(-4) = -13,75
в) х = -2
f(-2) = (-2)² -8*(-2)/(-2+1) = 20/(-1) = -20
4) maxf(x) = f((-2) = -20
minf(x) = f(-4) = -24