 натуральное число, тогда
натуральное число, тогда 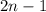 будет натуральным и нечётным числом. Возведем данное число в квадрат:
будет натуральным и нечётным числом. Возведем данное число в квадрат: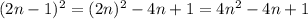

 , 0 делиться на 8, следовательно условие выполняется.
, 0 делиться на 8, следовательно условие выполняется. . Докажем что данное число делиться на 8 при
. Докажем что данное число делиться на 8 при 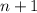 :
:
 делиться на 8. Следовательно, существует натуральный
делиться на 8. Следовательно, существует натуральный 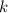 так что:
так что: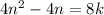
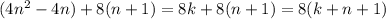 следовательно, при
следовательно, при 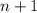 данное число тоже делиться на 8. Ч.Т.Д.
данное число тоже делиться на 8. Ч.Т.Д.
 натуральное число, тогда
натуральное число, тогда 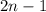 будет натуральным и нечётным числом. Возведем данное число в квадрат:
будет натуральным и нечётным числом. Возведем данное число в квадрат: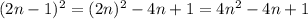

 , 0 делиться на 8, следовательно условие выполняется.
, 0 делиться на 8, следовательно условие выполняется. . Докажем что данное число делиться на 8 при
. Докажем что данное число делиться на 8 при 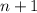 :
:
 делиться на 8. Следовательно, существует натуральный
делиться на 8. Следовательно, существует натуральный 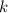 так что:
так что: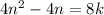
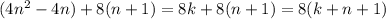 следовательно, при
следовательно, при 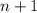 данное число тоже делиться на 8. Ч.Т.Д.
данное число тоже делиться на 8. Ч.Т.Д.
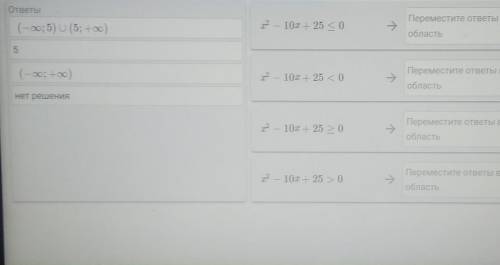
1. x^2-10x+25<=0
(x-5)^2<=0
x-5<=0
x<=5
x=5
2. x^2-10x+25<0
x-5<0
x<5
нет решения
3. x^2-10x+25>=0
(x-5)^2>=0
x-5>=0
x>=5
x=5
xe(-00;+00)
4. x^2-10x+25>0
x-5>0
x>5
(-00;5)U(5;+00)
Объяснение: Это ОДЗ