
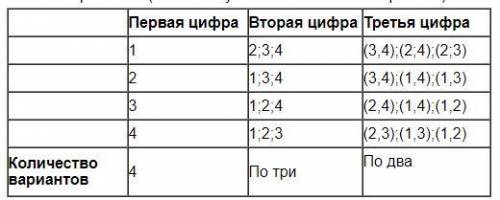
1) Сколько разных трехзначных чисел, не имеющих одинаковых цифр, можно записать с цифр 1, 2, 3, 4?
Схема решения (в скобках указаны возможные варианты):
Объяснение:
Значит, общее количество вариантов: 4*3*2 = 24 трехзначных числа.
2) Сколько разных трехзначных чисел можно записать с цифр 6,7,8,9?
Решение: 4*4*4 = 64 трехзначных числа.
3) Сколько разных двузначных чисел можно записать, используя 1, 2, 3, 4?
Решение: 4*4 = 16 двузначных чисел.
4) Какова вероятность того, что двузначное число, записанное цифрами 1, 2, является четным?
Решение: Р(А) = 2 :( 2*2) =0,5
5) Сколькими можно составить расписание из 4 разных предметов на один учебный день из четырех уроков?
Решение
Сколькими можно составить расписание из 6 разных предметов на один учебный день из шести уроков?
Решение
6) Сколькими можно составить расписание из 6 разных предметов на один учебный день из шести уроков так, чтобы первый урок был физика, а последний физкультура?
Решение
7) Сколькими можно составить расписание из 6 разных предметов на один учебный день из шести уроков так, чтобы первым уроком была физика, а перед последней физкультурой была алгебра?
Решение
8) Найти вероятность того, что в расписании на один учебный день из шести уроков из шести разных предметов вторым уроком была химия.
Решение: Р(А) = (5*1*4*3*2*1) : (6*5*4*3*2*1) = 1/6
9) Из пяти спортсменов для участия в турнире нужно послать троих. Сколькими это можно сделать?
Решение: С
10) Сколькими из 36 карт можно выбрать две карты?
Решение: С
11) На окружности отмечено 12 точек. Сколько существует треугольников с вершинами в этих точках?
Решение: С312= 12! : (9!*3!)=223 треугольников
12) В вазе лежат 5 разных яблок и 6 разных апельсин. Сколькими из них можно выбрать два яблока и два апельсина?
Решение: С25* С
13) В школьном хоре 6 девочек и 4 мальчика, в том числе Миша Орлов. Какова вероятность, что в концерте будет участвовать Миша, если в концерте будет участвовать один мальчик и одна девочка?
Решение: Р (А) = 6 : (С16* С14) = ¼
Целесообразно бывает при изучении комбинаторных эадач параллельно рассматривать задачи по теории вероятностей, тем самым показывая во-первых тесную связь этих тем, а во- вторых более рациональное их решение. Задачи, в которых рассматривается количество соединений разных элементов, можно начинать с 5 класса на факультативных, кружковых занятиях, при обобщающем повторении и на предметных неделях, циклично возвращаясь к ним на протяжении всего курса до 11 класса, углубляя знания по данным темам год от года.
Тогда к 11 классу учащиеся уверенно вычисляя факториалы натуральных чисел, будут находить вероятности событий и отвечать на вопросы комбинаторных задач, не испытывая дискомфорта или страха перед нестандартными учебными задачами.
a) 5[x]*5[3x]=5[4x]( Объяснение : x=1 3x=3x 3x+1=4x =5[4x] )
b) 2[x]*4[x]*8[x]=2[6x] ( Объяснение : Записать число в виде степени с основанием 2 4[x] ---> (2[2]) 4[x] упростить выражение путем умножения показателей степеней 2[2x] 2[x]*4[x]*8[x]= 4[x] = 2x[2x] =
2[x]*2[2x]*8[x], запешите выражение 8[x] в виде степени с основанием 2 2[3x] = 2[x]*2[2x]*2[3x] Вычислить = 2[6x] )
d) 3[x]+2:(9*3[x])= 3[2x+2]+2
3[x+2]
e) 3[x] * 3[2x]
27[x]
( Объяснение : Вычислить и сократить дробь = )
3[3x]
3[3x]
Делим.
=1
g) 5[x+1]*5[x]
25[x]
( Объяснение : Вычислить и сократить дробь 25 на 5= 5 )
=5
h) 7[2x]*7[2x]
49[x]
(Объяснение : Вычислить и сократить дробь 49 на 7 = 7 2x=2x = 7[2x].)
= 7[2x]
j) 4[x] * 2[2x] * 3[-3x] * 27x
8[2x]
=
x
3[3x-3]*4[x]
k) 5[3x]+5[x]
5[2x]+1
= 5[x]