Задание 1. Последовательность задана формулой . Определите номер члена последовательности равного . [2] Задание 2. Пусть есть арифметическая прогрессия. Если и , oпределите значение девятого члена прогрессии. [4] Задание 3. – геометрическая прогрессия 0,8; 0,2;… Найдите следующие два члена прогрессии. [3] Задание 4. ( ) – геометрическая прогрессия, если ; Найдите .
Оно, на первый взгляд, кажется очень сложным: здесь и шестая степень, и две неизвестные. Однако, как это всегда бывает, ответ всегда лежит на поверхности. Также и это уравнение можно легко решить, причем в данном случае x и y определены однозначно!
Для начала заметим, что .
Учитывая это перепишем уравнение:Теперь выполним хитрое преобразование:
Обращаем внимание на то, что равенство верно только, если , а .
Тогда решением исходного уравнения является пара чисел .
Первоначальная цена товара (х) руб после повышения стоимости на 18% цена товара: (1.18х) руб после снижения стоимости на 14% цена товара составила 86% от текущей стоимости (86=100-14) 0.86*1.18х = 1.0148х ответ: первоначальная цена товара увеличилась на 1.48% например, товар стоил 250 руб 18% от 250 руб --- это 45 руб после повышения цена составила 250+45 = 295 руб 14% от 295 руб --- это 41.3 руб после понижения цена составила 295-41.3 = 253.7 (руб) цена выросла на 3 рубля 70 копеек))) 250 руб 100% 3.7 руб ??% 3.7*100/250 = 370/250 = 37/25 = 1.48(%)
(см. объяснение)
Объяснение:
Рассмотрим уравнение:
Оно, на первый взгляд, кажется очень сложным: здесь и шестая степень, и две неизвестные. Однако, как это всегда бывает, ответ всегда лежит на поверхности. Также и это уравнение можно легко решить, причем в данном случае x и y определены однозначно!
Для начала заметим, что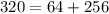
.
Учитывая это перепишем уравнение:
Теперь выполним хитрое преобразование:
Обращаем внимание на то, что равенство верно только, если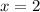
, а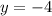 
.
Тогда решением исходного уравнения является пара чисел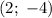
.
Уравнение решено!