y=x(x+2)-6x при x≥0
y=(-x)(x+2)-6x при x<0
y=x2+2x-6x при x≥0
y=-x2-2x-6x при x<0
y=x2-4x при x≥0
y=-x2-8x при x<0
1) y=x2-4x, при x≥0
Графиком подфункции - парабола.
Ветви направлены вверх.
x^2-4x=0
x(x-4)=0
x1=0 x-4=0
x2=4
2) y=-x2-8x, при x<0
График подфункции - парабола.
Ветви направлены вниз
-x2-8x=0
-x(x+8)=0
x1=0
x+8=0
x2=-8
Первый график у нас получается y=x2-4x, при x≥0
Второй график: y=-x2-8x, при x<0
Прямая: y=m
Две точки пересечения будет только когда прямая будет касаться вершин парабол.
Найдем координату Y вершин парабол, это и будут m, при которых прямая y=m будет иметь только две точки пересечения с графиком.
1) Для первой подфункции x0=-b/(2a)=-(-4)/(2*1)=4/2=2
y0=-5,25
2) Для второй подфункции x0=-b/(2a)=-(-8)/(2*(-1))=8/(-2)=-4
y0=(-4)2-8*(-4)=24
ответ: m1=-5,25, m2=24
вроде так!
Объяснение:
1.
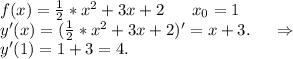
ответ: y'(1)=4.
2.

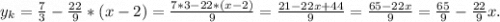
3.
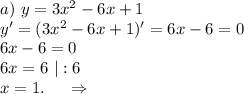
В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.
При х∈(-∞;1) функция убывает.
При х∈(1;+∞) фунуция возрастает .
![b)\ y=x^9-9x\\y'=(x^9-9x)'=9x^8-9=9*(x^8-1)=0\\9*(x^8-1)=0\ |:9\\x^8-1=0\\x^8=1\\x=\sqrt[8]{1}\\x_1=-1\ \ \ \ x_2=1](/tpl/images/1848/3010/401ca.png)
В окрестности точки x = -1 производная функции меняет знак с (+) на (-). Следовательно, точка x = -1 - точка максимума.
При х∈(-∞;-1) фунуция возрастает .
В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.
При х∈(1;+∞) функция возрастает. ⇒
При х∈(-1;1) функция убывает.
Параллельны
Объяснение:
Графики в условии заданы линейной ф-ей вида у=kx+b, где k- угловой коэффициент, а b-свободный член. Если угл. коэффиц равны, а свобод. члены отличаются, то гр-ки параллельны. Если угл. коэф равны и своб чл равны, то гр-ки совпадают. Если угл коэф разные, то при любых своб чл гр-ки пересекаются.
В данном случае угл коэф равны (5=5), свобод чл отличаются 0не=2, отсюда вывод: гр-ки параллельны