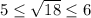
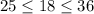
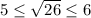. Возведя все части неравенства в квадрат, получим 
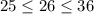. Неравенства выполняются, следовательно, число √26 заключен между числа 5 и 6.
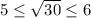. Возведя все части неравенства в квадрат, получим: 
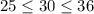. Видим, что неравенства правильны, следовательно, число √30 заключен между числа 5 и 6.
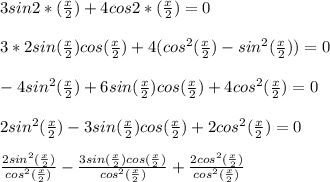=0
,
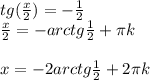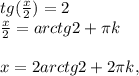
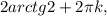k∈Z;
k∈Z.
19sin2x + 6cos^2x - 12 = 0
19*2sinxcosx+6cos^2x - 12(cos^2x+sin^2x) = 0
-12sin^2x+38sinxcosx-6cos^2x=0 /:(-2)
6sin^2x-19sinxcosx+3cos^2x=0 /:cos^2x≠0
6tg^2x-19tgx+3=0
tgx=t
6t^2-19t+3=0
D=289
t=3
t=1/6
x=arctg(3)+pik, k∈Z
x=arctg(1/6)+pik, k∈Z
9cosx + sinx - 1 = 0
подстановка tg(x/2)=t
9*(1-t^2)/(1+t^2)+2t/(1+t^2)-1=0
9*(1-t^2)+2t-(1+t^2)=0
9-9t^2+2t-1-t^2=0
-10t^2+2t+8=0 /:(-2)
5t^2-t-4=0
D=1+16*5=81
t=(1+9)/10=1
t=(1-9)/10=-8/10=-4/5
tg(x/2)=1
x/2=pi/4+pik /*2
x=pi/2+2pik
tg(x/2)=-4/5
x/2=-arctg(4/5)+pik
x=-2arctg(4/5)+2pik