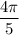Дугу можно измерять угловой мерой (размер центрального угла, опирающего на дугу) или длиной (угловая мера умноженная на радиус). Числовая окружность имеет радиус 1, поэтому значение угловой меры численно равно значению длины.
Половина окружности это π и это же длина дуги (для числовой окружности).
1. у = -2х² + 5х + 3 у=-4 -4=-2x²+5x+3 2x²-5x=7 2x²-5x-7=0 D=(-5)²-4*2*(-7)=81 √81=9 x₁=(5+9)/2*2=14/4=3.5 y=-4 при x₁=3.5; x₂=-1 x₂=(5-9)/2*2=-4/4=-1 2. f(x)= х² – 2х – 8 График во вложении а. y>0 при x∈(-∞;-2)∪(4;+∞) y<0 при x∈(-2;4) б. f возрастает (x₂>x₁ => y₂>y₁) при x∈(1;+∞) f убывает (x₂>x₁ => y₂<y₁) при x∈(-∞;1) в. y(max)=∞ y(min)=-9 3. у = -5х² + 6х Парабола y=ax²+bx, a<0, значит ветви параболы направлены вниз. y(min)=-∞ y(max) принадлежит вершине параболы: х=-b/2a => x=-6/2*-5=0.6 y=-5*0.6²+6*0.6 => y=1.8 Координаты вершины (0.6;1.8) y(max)=1.8 4. Для нахождение точек пересечения 2-х графиков, решаем систему уравнений: {у = х + 2 {у = ( х – 2)² + 2 x²-4x+4+2=x+2 x²-5x+4=0 x₁+x₂=5 x₁*x₂=4 x₁=4 x₂=1 y₁=4+2=6 y₂=1+2=3 Точки пересечения: (4;6) и (1;3) Для графического решения, чертим грапфики обеих функций в одной кооординатной плоскости. График во вложеннии
Дугу можно измерять угловой мерой (размер центрального угла, опирающего на дугу) или длиной (угловая мера умноженная на радиус). Числовая окружность имеет радиус 1, поэтому значение угловой меры численно равно значению длины.
Половина окружности это π и это же длина дуги (для числовой окружности).
∪AC = π = 2·∪AB ⇒ ∪AB =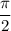
Пусть ∪AM = , тогда ∪MB =
, тогда ∪MB = 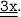
Т.к. первая четверть это ∪AB.
∪AM + ∪MB = 2x+3x = 5x =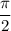 ⇒
⇒
x =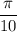 ⇒
⇒ 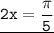 ;
; 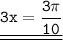
∪DM = ∪DA + ∪AM =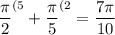
∪MC = ∪MB + ∪BC =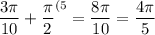
ответ: длина ∪AM =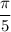
длина ∪MB =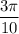
длина ∪DM =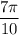
длина ∪MC =