Пример
Последовательность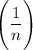 
монотонно стремится к нулю, поэтому по признаку Лейбница ряд сходится. Найдем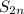 
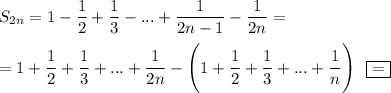
Выпишу формулу Эйлера)))) Пусть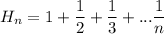 
. Эйлер получил асимптотическое выражение для суммы первых n членов ряда:
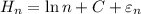
где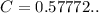 
- постоянная Эйлера, при 
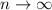значение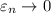 
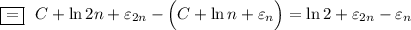
Следовательно,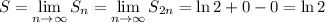 
- последовательность частичных сумм данного ряда.
Это мы показали что тот ряд равен ln 2. Теперь перейдем к нашем заданию.
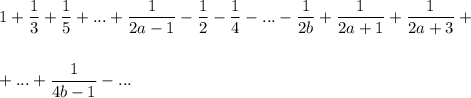
В силу примера, что мы показали в начале, мы получим
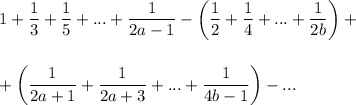
Первые две скобки - ряда сходятся, теперь нужно показать что последнее тоже сходится. Рассмотрим ряд
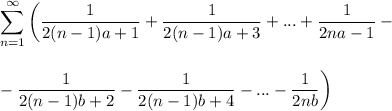
Пусть a > b, тогда
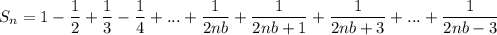
Тут (Sn) - последовательность частичных сумм исследуемого ряда.
Прибавляя и вычитая в выражение слагаемое, мы получим
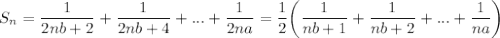
По формуле Эйлера
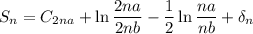
Переходя к пределу при n стремящихся к бесконечности, мы получим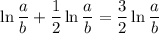 
Для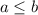 
аналогичным образом получается тот же результат. В частности если a = 2, b = 1, получим
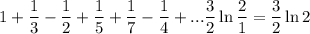
Подкоренное выражение 7х - х² должно быть положительным или равным нулю, потому что извлекать квадратный корень из отрицательного числа нельзя.
7х - х² ≥ 0.
Решим неравенство методом интервалов. Найдем нули функции.
7х - х² = 0.
Вынесем за скобку общий множитель х.
х(7 - х) = 0.
Произведение двух множителей равно нулю тогда, когда один из множителей равен нулю.
1) х = 0;
2) 7 - х = 0;
х = 7.
Отметим на числовой прямой точки 0 и 7.
Эти числа делят числовую прямую на интервалы 1) (-∞; 0], 2) [0; 7], 3) [7; +∞).
Выясним, на каком из интервалов выражение 7х - х² будет принимать положительные значения. На 1 и 3 интервалах это выражение отрицательно, на 2 итервале - положительно. Поэтому, значения х, принадлежащие 2 интервалу являются областью определения функции.
ответ. [0; 7].
ответ:-17
Объяснение:отбичаю дұрыс