


y = log₂(-x² + 4x + 5) + 2
ОДЗ : -x² + 4x + 5 > 0
-(x² - 4x - 5) > 0 ⇔ x² - 4x - 5 < 0 ⇔
(x - 5)(x + 1) < 0
Метод интервалов
+++++++ (-1) -------- (5) ++++++++ >>> x
ОДЗ : x ∈ (-1; 5)
y = log₂(-x² + 4x + 5) + 2 = log₂(-x² + 4x + 5) + log₂4 =
= log₂ ( ( -x² + 4x + 5) * 4) = log₂( -4x² + 16x + 20)
y = log₂( -4x² + 16x + 20) - логарифмическая функция с основанием 2 > 1
⇒ большему значению аргумента соответствует большее значение функции, т.е. достаточно найти наибольшее значение выражения под логарифмом, чтобы найти максимум логарифмической функции.
f(x) = -4x² + 16x + 20 - квадратичная функция.
График - квадратичная парабола, ветви направлены вниз.
Точка максимума - вершина параболы
Координата вершины параболы
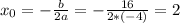
x₀ = 2 ∈ ОДЗ ⇒
x₀ = 2 - точка максимума функции y = log₂(-x² + 4x + 5) + 2
Максимальное значение функции :y(2) = log₂(-2² + 4*2 + 5) + 2 = log₂9 + 2 = 2( log₂3 + 1)
ответ: точка максимума х₀ = 2
2)=10х^2-8х+15х-12=10х^2+7х-12
3)=3х^2+12х-2х-8=3х^2+10х-8
4)=20а^2-5аб-4аб+б^2=
=20а^2-9аб+б^2
5)=4м^2-10мн+6мн-15н^2=
=4м^2-4мн-15н^2
6)=8р^2+5рф-24рф-15ф^2=
=8р^2-19рф-15ф^2
7)=ху+хм+му+м^2
8)=4х^2+2ху-2х-у
9)=ау+2а-у^2-2у
10)=12а^4-24а^2б^2+10а^2б^2-20б^4=12а^4-14а^2б^2-20б^4
11)=7м^4-21м^2н^2+8м^2н^2-24н^4=7м^4-13м^2н^2-24н^4
12)=4н^4+20н^2-н^2+5=
=4н^4+19н^2+5
13)=24х^5-8х^3у-9х^4у+3х^2у^2
14)=15а^2б^5-12аб^6
16)=а(х+у)+б(х+у)=(а+б)(х+у)
17)=а(а+б)+с(а+б)=(а+с)(а+б)
19)=х(х+у)+а(х+у)=(х+а)(х+у)
20)=х^2(х+3)+3(х+3)=(х^2+3)(х+3)
22)=м(м+н)-5(м+н)=(м-5)(м+н)
24)=5х(х-а)+7(х-а)=(5х+7)(х-а)
25)=4х(х-з)-3(х-з)=(4х-3)(х-з)