Обозначим x,y,z длины каждого из отрезков.
Тогда:
x=0,25*y (отрезок х в 4 раза меньше чем отрезок у)
x=z+1 (отрезок х на 1 см больше чем отрезок z)
x+y+z=35
Объединяем все условия в одно и получаем систему:
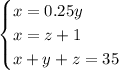
Немного преобразуем ее и получим:
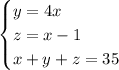
Подставим получившиеся выражения для y,z в последнее уравнение и получим:
x+4x+x-1=35
6x=36
x=6
Теперь найдем y и z
Получаем:
y=4*6=24
z=6-1=5
Получили решение: x=6, y=24, z=5
Теперь проверим соответсвует ли найденное решение нашим условиям:
(это надо просто устно сделать)
Действительно длина одного из отрезков (в данном случае х) в 4 раза меньше длиный другого (в данном случае у) и на 1 больше чем длина третьего (в данном случае z)
В сумме их длины дают 35 (6+24+5=35)
Значит решили верно
Длина первого отрезка = 6
Длина второго отрезка = 24
Длина третьего отрезка = 5
Обозначим x,y,z длины каждого из отрезков.
Тогда:
x=0,25*y (отрезок х в 4 раза меньше чем отрезок у)
x=z+1 (отрезок х на 1 см больше чем отрезок z)
x+y+z=35
Объединяем все условия в одно и получаем систему:
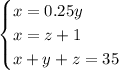
Немного преобразуем ее и получим:
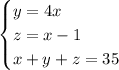
Подставим получившиеся выражения для y,z в последнее уравнение и получим:
x+4x+x-1=35
6x=36
x=6
Теперь найдем y и z
Получаем:
y=4*6=24
z=6-1=5
Получили решение: x=6, y=24, z=5
Теперь проверим соответсвует ли найденное решение нашим условиям:
(это надо просто устно сделать)
Действительно длина одного из отрезков (в данном случае х) в 4 раза меньше длиный другого (в данном случае у) и на 1 больше чем длина третьего (в данном случае z)
В сумме их длины дают 35 (6+24+5=35)
Значит решили верно
Длина первого отрезка = 6
Длина второго отрезка = 24
Длина третьего отрезка = 5
ответ: q = - 24.
Объяснение:
Теорема Виета для приведённых квадратных уравнений вида x^2 + px + q = 0, гласит что справедливы следующие отношения:
х1 + х2 = - p;
x1 * x2 = q,
где x1 и х2 — корни приведенного квадратного уравнения.
Согласно теореме Виета найдем q для уравнения корнями которого являются числа - 6 и 4.
q = - 6 * 4 = - 24.
ответ: q = - 24.