1. Общее число исходов равно числу сочетаний из 36 по 2:
n = С(36,2) = 36!/(33!*2!) = 34*35*36/2 = 21420
Благоприятные исходы - это когда обе карты - тузы, т.е. выбираются из 4
тузов: m = C(4,2) = 4!/(2!*2!) = 3*4/2 = 6
Р = m/n = 6/21420 = 1/3570
2. Элементарный исход в этом опыте - упорядоченная пара чисел. Первое число
выпадает на первом кубике, второе - на втором. Множество элементарных исходов удобно представить таблицей: 11 21 31 41 51 61
12 22 32 42 52 62
13 23 33 43 53 63
14 24 34 44 54 64
15 25 35 45 55 65
16 26 36 46 56 66 Получено 36 исходов, т.е. n = 36. Из них нас интересуют только те, в которых сумма цифр равна 10. Из таблицы видно, что таких вариантов всего 3: 46, 55, 64. m = 3 Значит искомая вероятность равна: Р = m/n = 3/36 = 1/12.
3. Сначала подсчитаем вероятность того, что две карты окажутся одной масти. Пусть А - появление первой карты определенной масти, В - появление второй карты той же масти. Событие В зависит от события А, т.к. его вероятность меняется от того, произошло или нет событие А. Поэтому: Р(АВ) = Р(А)*Р(В\А) = 9/36 * 8/35 = 1/4 * 8/35 = 2/35 Т.к. в колоде 4 различные масти, то вероятность, что обе карты окажутся одной масти равна: Р = 2/35 + 2/35 + 2/35 + 2/35 = 8/35
4. Аналогично задаче № 2. Множество элементарных исходов n = 36. Из них нас интересуют только те, в которых сумма цифр равна 6. Из таблицы видно, что таких вариантов всего 5: 15, 24, 33, 42, 51. m = 5 Значит искомая вероятность равна: Р = m/n = 5/36.
В обоих случаях рассматриваем прямоугольный треугольник с одним из углов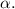 
В первом случае примем прилежащий к углу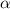 
катет за 3, а гипотенузу - за 5. Тогда неизвестный катет вычислим по т. Пифагора как 
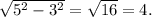Синус угла 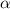есть отношение противолежащего катета к гипотенузе, т.е. 4/5. Тангенсом - отношение противолежащего катета к прилежащему, т.е. 4/3. Котангенсом - отношение прилежащего катета к противолежащему, т.е. 3/4.
Во втором случае примем катет, лежащий против 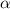за 4, а гипотенузу - за 5. Неизвестный катет, по теореме Пифагора, будет равен 3. Косинусом 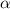есть отношение прилежащего катета к гипотенузе, т.е. 3/5. Тангенсом - отношение противолежащего катета к прилежащему, т.е. 4/3. Котангенсом - отношение прилежащего катета к противолежащему, т.е. 3/4.
Уранвение тогда будет иметь 2 корня когда дискриминант больше 0.В соответствии с этим составляем уравнение:
Берем там где больше значений,а значит k>-2/Это все его значения