Question

Найдите остаток от деления 3^2020 на

Answer 1

1

Объяснение:

Найдём функцию Эйлера от числа 5. Это количество чисел, меньших 5 и взаимно простых с ним, то есть не имеющих с 5 общих делителей. Такими числами являются 1, 2, 3, 4, поскольку они не делятся на 5. Тогда функция Эйлера φ(5) = 4 (к тому же функция Эйлера простого числа, каким является 5, представляет собой результат вычитания единицы из этого числа, то есть 5 - 1 = 4, как у нас и получилось).

Так как 3 и 5 — взаимно простые числа, то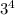 $3^{4}$ сравнимо с 1 по модулю 5.

2020 = 5 * 404

Тогда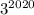 $3^{2020}$ можно записать в виде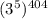 $(3^{5}) ^{404}$

Поскольку мы выяснили, что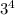 $3^{4}$ сравнимо с 1 по модулю 5, то 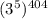$(3^{5}) ^{404}$ также сравнимо с 1 по модулю 5. То есть остаток равен 1.