На почеркушки не обращайте внимание
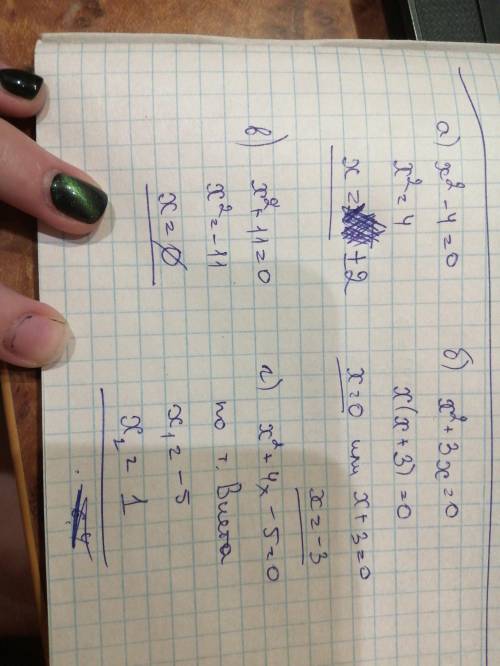

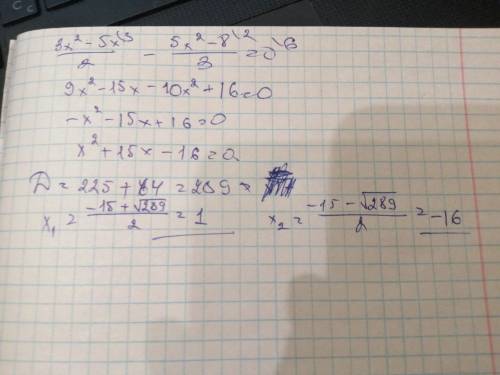
Объяснение:
ОДЗ : cos2x ; sin2x
cosx ± 1/4 ; sinx ; cosx 0
x ± arccos0,25 + 2πk ; x πk/2 , k ∈ z
2*2cos^2 x - 2 = 1/2cos2x * ( ... )
2cos2x = 1/2cos2x * ( ... )
можно поделить на cos2x, так как cos2x также есть в знаменателе, то есть корни мы не теряем
2 = 1/2 * ( ... )
для удобства делаем замену: пусть 2x = t
2 = 1/2 * (/cost + 1/sint)
2 = /2cost + 1/2sint
(sint + cost) / 2costsint = 2
-2 (-/2 sint - 1/2 cost) / 2costsint = 2
-2 (-sin (π/3) sint - cos(π/3) cost) / 2costsint = 2
выносим минус за скобки и сокращаем 2
а также, используя формула приведения косинуса, только в обратную сторону, делаем все красиво
cos (π/3 - t) / costsint = 2
cos (π/3 - t) = 2costsint
cos (π/3 - t) - sin2t = 0
sin (π/2 - (π/3 - t) - sin2t = 0
sin (π/6 + t) - sin2t = 0
используем sin(t) - sin(s) = 2cos((t + s)/2) * sin ((t - s)/2)
и делим на 2
cos ((π + 18t)/12) * sin((π - 6t)/12) = 0
cos ((π + 18t)/12) = 0
sin ((π - 6t)/12) = 0
t = 5π/18 + 2πk/3
t = π/6 + 2πk
вспоминаем, что t = 2x
x = 5π/36 + πk/3
x = π/12 + πk
k ∈ Z
Первая картинка
а) 2 и -2
б)0 и -3
в)нет решений
г)1 и -5
д)3,5 и -1
Вторая картинка
а)4
б)-16 и 1
Объяснение:
Первая картинка
а) х²-4=0
формула сокращённого умножения, раскладывается как
(х+2)(х-2)=0
Произведение чисел равняется нулю, только когда один из множителей равняется нулю
х-2 равняется 0 при х=2,
х+2 равняется 0 при х= -2
Это значит, что уравнение имеет 2 корня: 2 и -2
б)х²+3х=0
выносим х за скобки
х(х+3)=0
Произведение чисел равняется нулю, только когда один из множителей равняется нулю
х равняется 0 при х=0
х+3 равняется 0 при х = -3
Это значит что уравнение имеет 2 корня: 0 и -3
в)х²+11=0
Переносим известные мне неизвестные влево
х²= -11
Квадрат числа не может быть отрицательным т.к чтобы возвести в квадрат
отрицательное число надо перемножить 2 отрицательных, в результате чего получится положительное число, чтобы возвести в квадрат положительное число надо перемножить 2 положительных, в результате чего получится положительное число, чтобы возвести в квадрат 0 надо перемножить 2 нуля, в результате чего получится 0, который не является отрицательным числом.
Уравнение не имеет корней
г)х²+4х-5=0
найдем дискриминант
D=16+20=36
найдем корни уравнения
х1,х2=(-4±√D)/2
x1=1
x2= -5
уравнение имеет 2 корня: 1 и -5
д)2х²-5х-7=0
Найдем дискриминант
D=25+56=81
найдем корни уравнения
х1,х2=(5±√D)/4
x1=3,5
x2= -1
Уравнение имеет 2 корня: 3,5 и -1
Вторая картинка
а)(х-5)²+(х-3)²=2
Тут две формулы сокращённого умножения раскладывается как
х²-10х+25+х²-6х+9=2
2х²-16х+34=2
Переносим 2 влево
2х²-16х+34-2=0
2х²-16х+32=0
Поделим обе стороны равенства на 2
х²-8х+16=0
найдем дискриминант
D=64-64=0
Найдем корень уравнения
х=8/2=4
Уравнение имеет 1 корень: 4
б)(3х²-5х)/2-(5х²-8)/3=0
приведем дроби к общему знаменателю
(9х²-15х)/6-(10х²-16)/6=0
(9х²-15х-10х²+16)/6=0
(-х²-15х+16)/6=0
Частное равно нулю только тогда когда делимое равно нулю
-х²-15х+16=0
найдем дискриминант
D=225+64=289
найдем корни уравнения
х1,х2=(15±√D)/-2
x1= -16
x2= 1
Уравнение имеет 2 корня:1 и -16