Должно выполняться условие, что суммы противоположных сторон четырехугольника равны - только тогда получиться вписать в него окружность.
Распишем это условие: ⇔ . где a - боковые стороны, b и c - основы.
Сделаем вывод, что трапеция являеться равнобедренной.
Формула для нахождения площади через среднюю линию и высоту трапеции: ⇔ , где S - площадь трапеции, m - средняя линия трапеции, h - ее высота. , b и c - основы трапеции.
Зная радиус вписаной окружности, мы знаем высоту трапеции: ⇔ .
Соответственно, из прямоугольного треугольника ADH1 найдём боковую сторону трапеции с соотношений: ⇒ см - боковая сторона трапеции.
Если , то зная а = 8, можем найти среднюю линию, а соответственно и площадь. см.
Последнее воскресенье перед последним понедельником в одном городе, а совсем последнее воскресенье в другом городе. Это значит, что воскресенье было последним днём месяца. А в следующем месяце было тоже самое - воскресенье было последним днём месяца. Это значит, что второй месяц был невисокосный февраль, а первый январь. Итак, 31 января Игорь был в Мурманске, а 31-7=24 января в Новосибирске. В следующем месяце, феврале, 28 он был в Томске, а за неделю до этого, 21 февраля в Кирове. Остаётся добавить, что последний раз 31 января и 28 февраля выпали на воскресенье в 2010 г.
S = 64 см²
Объяснение:
r = 4 см
S - ?
=============
Должно выполняться условие, что суммы противоположных сторон четырехугольника равны - только тогда получиться вписать в него окружность.
Распишем это условие:
⇔ 
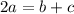. где a - боковые стороны, b и c - основы.
Сделаем вывод, что трапеция являеться равнобедренной.
Формула для нахождения площади через среднюю линию и высоту трапеции: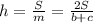
⇔ 
, где S - площадь трапеции, m - средняя линия трапеции, h - ее высота. 
, b и c - основы трапеции.
Зная радиус вписаной окружности, мы знаем высоту трапеции:
⇔ 
.
Соответственно, из прямоугольного треугольника ADH1 найдём боковую сторону трапеции с соотношений: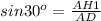
⇒ 
см - боковая сторона трапеции.
Если
, то зная а = 8, можем найти среднюю линию, а соответственно и площадь.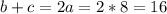 
см.
Просто подставляем в формулу площади: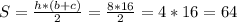
см².