1) Используя формулу n-го члена арифметической прогрессии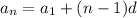 
, вычислим двадцатый член этой прогрессии:
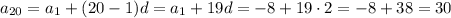
ответ: 30.
2) Формула суммы первых n членов арифметической прогрессии следующая: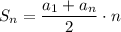 
Найдем же сначала восемнадцатый член арифметической прогрессии
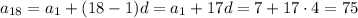
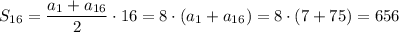
ответ: 656.
3) Первый член: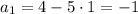 
Второй член: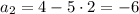 
Третий член: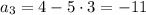 
Как видно, каждый последующий член уменьшается на (-5),т.е. это разность d = -5, следовательно, последовательность является арифметической прогрессией.
4) Используя n-ый член арифметической прогрессии, найдем ее разность
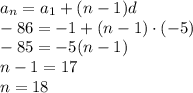
Да, является арифметической прогрессией.
5) Данная последовательность является арифметической прогрессии с первым членом 
и разностью прогрессии d=1
Всего таких членов не трудно посчитать по формуле n-го члена арифметической прогрессии:
То есть, нужно посчитать сумму первых 91 членов арифметической прогрессии
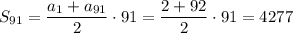
ответ: 4277.
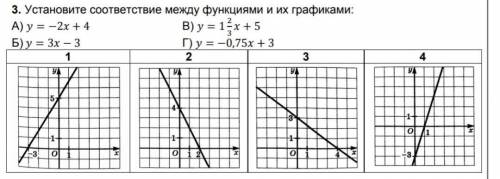
1.(В) 2. (А) 3. (Г) . 4. (Б)
Объяснение:
Ну вроде бы должно быть так
Но я точно не уверена