6543 и 6210
Объяснение:
Рассматриваются четырёхзначные числа M, среди которых нужно выбрать числа, удовлетворяющие условиям:
1) 6000 < M < 7000;
2) M делится на 9;
3) каждая следующая цифра M меньше предыдущей.
Если представить число M в виде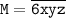 
, где хотя-бы один из цифр x или y или z отличен от 0, то 1-условие выполнено. Но, если выполняется 3-условие, то есть если 6>x>y>z, то 1-условие выполняется.
Рассмотрим все числа вида 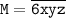, для которых выполнено 3-условие:
6543, 6542, 6541, 6540, 6532, 6531, 6530, 6521, 6520, 6510;
6432, 6431, 6430, 6421, 6420, 6410;
6321, 6320, 6310;
6210.
Остается проверить 2-условие для этих чисел. Используем признак делимости на 9:
Число А делится на 9 ⇔ Сумма цифр числа А делится на 9.
Нетрудно проверить, что только следующие числа делятся на 9:
6543 (6+5+4+3=18) и 6210 (6+2+1+0=9).
3x = 12
x = 4
2)12 - 2x = - 10
- 2x = - 22
x = 11
3)2x + 3 = 10
2x = 7
x = 3,5
4) 14x - 7 = 28
14x = 35
x = 2,5
5) (x - 3)(15 - x) = 0
15x - x² - 45 + 3x = 0
- x² + 18x - 45 = 0
x² - 18x + 45 = 0
D = b² - 4ac = 324 - 4×45 = 324 - 180 = √144= 12
x₁ = 18 + 12/2 = 15
x₂ = 18 - 12/2 = 3
6) (2x - 20)(3 + 3x) = 0
6x + 6x² - 60 - 60x = 0
6x² - 54x - 60 = 0
D = 2916 - 4×6 × ( - 60) = 2916 + 1440 = 4356
x₁ = 54 + 66/ 12 = 10
x₂ = 54 - 66/12 = - 1
7)( 12 - 3x)(25 - 5x) =0
300 - 60x - 75x + 15x² = 0
15x² - 135x + 300 = 0
D = 18225 - 4 × 15 × 300 = 18225 - 18000 = √225 = 15
x₁ = 135 + 15/30 = 5
x₂ = 135 - 15/30 = 4