
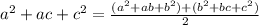

а) модуль числа а это само число а, если оно взято со знаком + и число !а!=-а, если а число отрицательное, т.е. взято со знаком -. Отсюда можно сделать вывод что модуль никогда не может быть равен отрицательному числу, абсолятное значение всегда положительно, поэтому единственное число, удоволтворяющее !x!=-x это 0, поэтому под буквой а можешь отметить только 0
б) Во втором случае этому уравнению будет эквивалентна система уравнений вида
x+2=x+2 - тождественно верно
x+2=-(x+2)-решаем
x+2=-x-2
x+x+2+2=0
2x+4=0
2x=-4
x=-2
Значит все точки числовой прямой начиная с x=-2 и в положительнную сторону будут удоволетворять уравнению, отсюда ответ будет вся числовая прямая начиная с -2 и больше
1 - n-й член
2 - знаменатель прогрессия
3 - сумма n первых членов
5. 0,(162)
Считаем число цифр в периоде k=3. В непериодической части после запятой m=0. Записываем все цифры числа а=162. Все цифры непериод. части после запятой - b=0. Cчитаем по формуле:
где девяток k, а нулей - m.
0,8(4) -аналогично.
k=1,m=1, a=84, b=8