Сумма квадратов цифр некоторого двухзначного числа равна 26. произведение данного числа на число, записанное теми же цифрами,но в обратном порядке, равно 765. найдите это число. желательно с решением
Пусть х-цифра десятков, а у - цифра единиц некоторого двузначного числа. Тогда само число 10х+у, а число записанное теми же цифрами в обратном порядке 10у+х. (10х+у)*(10у+х)-произведение чисел, - сумма квадратов цифр. По условию произведение равно 765, а сумма квадратов цифр 26. Получим систему уравнений:
Получим или или или
Так как х и у - цифры, то x>=0 и y>=0. Значит, или
Упростим функцию: y=x²+2 - квадратичная парабола, которую можно построить путем сдвига функции у=х² на две единицы вверх вдоль оси OY. у=х²: х -3 -2 -1 0 1 2 3 у 9 4 1 0 1 4 9 у=х²+2: х -3 -2 -1 0 1 2 3 у 11 6 3 2 3 6 11 График см. на рисунке.
Свойства: 1) Область определения: D=R. 2) Область значений: Е=[2;+∞). 3) Значение у=2 является наименьшим, наибольшего нет. 4) Функция чётная. 5) Функция непериодическая. 6) Точек пересечения с осью ОХ нет, т.е. нулей не имеет. 7) Точка пересечения с осью OY (0;2). 8) На промежутке (-∞;0] функция убывает, на промежутке [0;+∞) функция возрастает. 9) На всей области определения, т.е. на R функция принимает положительные значения.
Пусть х-цифра десятков, а у - цифра единиц некоторого двузначного числа. Тогда само число 10х+у, а число записанное теми же цифрами в обратном порядке 10у+х. (10х+у)*(10у+х)-произведение чисел,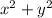 - сумма квадратов цифр. По условию произведение равно 765, а сумма квадратов цифр 26. Получим систему уравнений:
- сумма квадратов цифр. По условию произведение равно 765, а сумма квадратов цифр 26. Получим систему уравнений:
Получим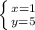 или
или 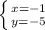 или
или 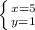 или
или 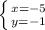
Так как х и у - цифры, то x>=0 и y>=0. Значит,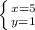 или
или 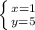
Итак, данное число либо 15, либо 51.
ответ: 15 или 51.