Найдём функцию Эйлера от числа 15. Это количество чисел, меньших 15 и взаимно простых с ним, то есть не имеющих с 15 общих делителей. Такими числами являются 1, 2, 4, 7, 8, 11, 13, 14, поскольку они не делятся ни на 3, ни на 5. Тогда функция Эйлера φ(15) = 8.
Так как 2 и 15 — взаимно простые числа, то сравнимо с 1 по модулю 15.
Тогда можно записать в виде
Поскольку мы выяснили, что сравнимо с 1 по модулю 15, то также сравнимо с 1 по модулю 15.
Остаётся , которое сравнимо с 8 по модулю 15, поскольку даёт остаток 8 при делении на 15.
Первый экскаватор выроет за 12 часов, второй за 6. Обозначим время, за которое первый экскаватор выроет котлован за х часов, тогда второй котлован выроет за (x-6) часов. За 1 час первый экскаватор выкопает 1/x часть котлована, а второй за 1 час выкопает 1/(x-6) часть котлована. А вместе за час по условию они выкопают 1/4 часть котлована (поскольку целиком они выкопают его вместе за 4 часа) . Имеем уравнение: 1/x+1/(x-6)=1/4 Квадратное уравнение: 4*x-24+4*x=x^2-6*x Приводим подобные: x^2-14*x+24=0 x1=12 (часов) x2=2 (часа) - посторонний корень, поскольку в этом случае время, за которое второй экскаватор выкопает котлован, будет отрицательным (2-6=-4), что не имеет физического смысла. Итак, первый экскаватор выкопает котлован за 12 часов, а второй за 12-6=6 часов ответ: Первый за 12, второй за 6 часов.
8
Объяснение:
Найдём функцию Эйлера от числа 15. Это количество чисел, меньших 15 и взаимно простых с ним, то есть не имеющих с 15 общих делителей. Такими числами являются 1, 2, 4, 7, 8, 11, 13, 14, поскольку они не делятся ни на 3, ни на 5. Тогда функция Эйлера φ(15) = 8.
Так как 2 и 15 — взаимно простые числа, то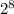 сравнимо с 1 по модулю 15.
сравнимо с 1 по модулю 15.
Тогда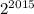 можно записать в виде
можно записать в виде 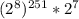
Поскольку мы выяснили, что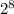 сравнимо с 1 по модулю 15, то
сравнимо с 1 по модулю 15, то 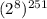 также сравнимо с 1 по модулю 15.
также сравнимо с 1 по модулю 15.
Остаётся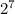 , которое сравнимо с 8 по модулю 15, поскольку даёт остаток 8 при делении на 15.
, которое сравнимо с 8 по модулю 15, поскольку даёт остаток 8 при делении на 15.
То есть можем записать: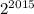 ≡
≡ 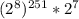 ≡
≡ 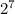 ≡ 8 mod 15
≡ 8 mod 15
Это значит, что остаток равен 8.