1)при каких значениях а выражение 12a+ 2 больше 10а-6? 2)при ткаких значениях b выражение 15b+ 6 меньше значения выражения 18+13b? решите систему: 3)2х+ 7≥или = 1 х-3< 1(объеденяет фигурная скобка). 4)4х+9> -15 2-х≤ 5(объединяет фигурная скобка).

👇

Увидеть ответ

Ответ:

ibatulina03

10.07.2021

1) 12a + 2 > 10a - 6

12a - 10 a > - 6 - 2

2a > - 8

a > - 4

ответ: от минуса 4 до плюс бесконечности

2) 15b + 6 < 18 + 13 b

15b - 13 b < 18 - 6

2b < 12

b < 6

ответ: от минуса бесконечность до 6

3)A) 2X + 7 > 1, 2x > -6, x > -3 (или=)

B) X - 3 < 1, X < 4

ответ: X принадлежит от минуса 3 (можем ему равняться) до 4 (ему не равен)

4) A) 4X + 9 > - 15, 4X > - 24, X > - 6

B) 2 - x < 5, X > - 3

ответ: от минуса 3 (ему равен) до минуса 6

4,8(90 оценок)

Открыть все ответы

Ответ:

Aizere1111

10.07.2021

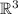Пусть $\varepsilon$ - канонический базис в $\mathbb{R}^{3}$ .

Тогда матрицу перехода 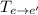$T_{e \rightarrow e'}$ можно найти следующим образом:

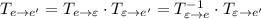
$T_{e \rightarrow e'} = T_{e \rightarrow \varepsilon} \cdot T_{\varepsilon \rightarrow e'} = T_{\varepsilon \rightarrow e}^{-1} \cdot T_{\varepsilon \rightarrow e'}$

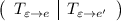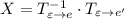
Если записать блочную матрицу $\left(\begin{array}{c|c}T_{\varepsilon \rightarrow e}&T_{\varepsilon \rightarrow e'}\end{array}\right)$ и привести путем элементарных преобразований к виду $\left(\begin{array}{c|c}E&X\end{array}\right)$ , то $X = T_{\varepsilon \rightarrow e}^{-1} \cdot T_{\varepsilon \rightarrow e'}$

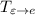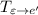Матрицу $T_{\varepsilon \rightarrow e}$ легко получить: достаточно записать в столбцы координаты векторов базиса . Аналогично с матрицей $T_{\varepsilon \rightarrow e'}$ .

В итоге необходимо получить вид $\left(\begin{array}{c|c}E&X\end{array}\right)$ следующей матрицы:

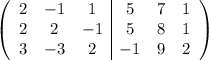
$\left(\begin{array}{ccc|ccc}2&-1&1&5&7&1\\2&2&-1&5&8&1\\3&-3&2&-1&9&2\end{array}\right)$

Вычтем первую строку из второй и третьей:

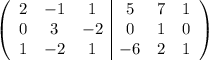
$\left(\begin{array}{ccc|ccc}2&-1&1&5&7&1\\0&3&-2&0&1&0\\1&-2&1&-6&2&1\end{array}\right)$

Вычтем из первой строки 2 третьих и поменяем их местами:

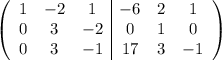
$\left(\begin{array}{ccc|ccc}1&-2&1&-6&2&1\\0&3&-2&0&1&0\\0&3&-1&17&3&-1\end{array}\right)$

Вычтем из третьей строки вторую:

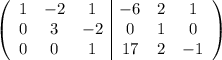
$\left(\begin{array}{ccc|ccc}1&-2&1&-6&2&1\\0&3&-2&0&1&0\\0&0&1&17&2&-1\end{array}\right)$

Прибавим ко второй строке 2 третьих и вычтем из первой третью:

$\left(\begin{array}{ccc|ccc}1&-2&0&-23&0&2\\0&3&0&34&5&-2\\0&0&1&17&2&-1\end{array}\right)$

Делим вторую строку на 3:

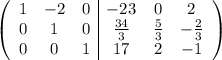
$\left(\begin{array}{ccc|ccc}1&-2&0&-23&0&2\\0&1&0&\frac{34}{3} &\frac{5}{3}&{-\frac{2}{3}}\\0&0&1&17&2&-1\end{array}\right)$

Прибавляем в первой строке 2 вторых:

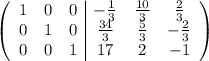
$\left(\begin{array}{ccc|ccc}1&0&0&{-\frac{1}{3}}&\frac{10}{3}&\frac{2}{3}\\0&1&0&\frac{34}{3} &\frac{5}{3}&{-\frac{2}{3}}\\0&0&1&17&2&-1\end{array}\right)$

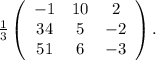
$\frac{1}{3}\left(\begin{array}{ccc}-1&10&2\\34&5&-2\\51&6&-3\end{array}\right).$

4,8(27 оценок)

Ответ:

Tiinker7

10.07.2021

192

Объяснение:

Чётные цифры: 0, 2, 4, 6, 8.

пятизначные числа не начинаются с 0, значит, на первом месте любая из четырёх цифр: 2, 4, 6, 8 На втором месте цифра 1 или 3, два варианта.

На третьем месте можно написать 0, но нельзя ту цифру, которая на первом месте. Цифры в записи числа не должны повторяться. Значит, четыре варианта для записи второй цифры.

На четвёртом месте цифра 5 или 7 - два варианта.

На пятом месте - чётная цифра, но не такая, как на первом и третьем - три варианта.

На шестом месте цифра 9 - один вариант.

По правилу произведения перемножаем возможные варианты постановки каждой цифры:

4⋅2⋅4⋅2⋅3⋅1=192

ответ: 192

4,8(36 оценок)

Это интересно:

Стиль-и-уход-за-собой

26.01.2020

Как отчистить сандалии Rainbow...

Стиль-и-уход-за-собой