Приймемо роботу за 1. х годин треба першому, в годин треба другому. перший за часом зробить 1 / х частина роботи, другий 1 / у. Разом за 6 годин вони зроблять (1 / х + 1 / у) * 6 або всю роботу; рівняння (1 / х + 1 / у) * 6 = 1
за 6 годин перший зробить 6 / г частину роботи, другий за 4 години 4 / в частина роботи, разом 6 / х + 4 / в або 0,8 роботи (80%); рівняння 6 / х + 4 / в = 0,8.
Об'єднати в систему:
6 / х + 6 / в = 1
6 / х + 4 / в = 0,8 віднімемо друге рівняння з першого
2 / в = 0,2 у = 10 (годин)
Підставами в перше рівняння і знайдемо х
6 / х + 6/10 = 1 6 / х = 4/10 х = 15 (годин)
Відповідь: першому треба 15 год, другого - 10 год.
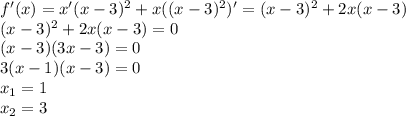
√x² = |x|
|x| = x x>=0
= -x x < 0
√(31 + 12√3) = √(4 + 2*2*3√3 + 27) = √(2² + 2*2*√27 + 27) = √(2 + √27)² = 2 + √27 = 2 + 3√3
√(9 - 4√5) = √(5 - 2*2*√5 + 4) = √(√5 - 2)² = {√5 - 2 > 0}=√5 - 2
√(13 - 4√3) = √(12 - 2*√12 + 1) = √(√12 - 1)² = (√12 - 1>0) =√12 - 1 = 2√3 - 1