
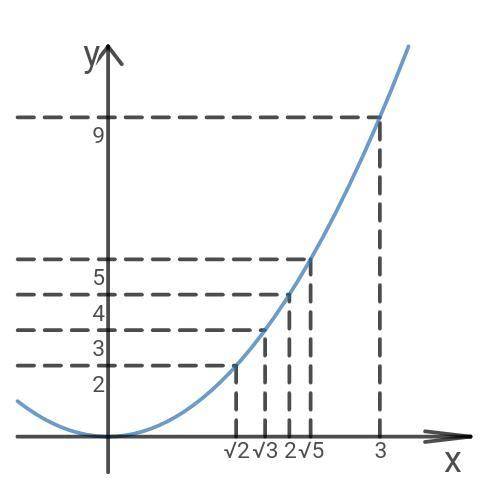
Построим схематично график функции y=x². Получится парабола с вершиной в начале координат, ветви параболы направлены вверх. В задании даны положительные числа, поэтому нас интересует часть графика в 1ой четверти. Определим квадраты данных чисел и проведём прямые y=a², где a - данное число (3²=9, (√5)²=5, 2²=4, (√3)²=3 и (√2)²=2).
Из точки пересечения прямой y=a² с графиком функции y=x², проведём перпендикуляр к оси Ox, точку пересечения с осью обозначим как соответствующее a.
Мы получили расположение данных чисел на числовой прямой x. Если число правее другого, то оно больше того же числа. Если число левее другого, то оно меньше того же числа.
1) √2 < 2
2) √2 < √3
3) √5 < 3
4) √3 < 2
№3
а) у=12 - 4х; переменной в знаменателе нет, как и самого знаменателя.
х - любое действительное число.
ИЛИ х∈(-∞; ∞)
б) переменная в знаменателе.
х-3≠0; х≠3; х - любое действ. число кроме 3.
ИЛИ х∈(-∞; 3)U(3; ∞).
№4
у=кх+в; у=(3х-2)/4; у=(3/4)*х - 1/2
к=3/4 > 0; график прямой идет вверх, функция возрастающая.
При х=-1 у=(-3-2)/4=-5/4=-1,25
При х=5 у=(15-2)/4=13/4=3 1/4=3,25
ответ: на промежутке -1<x≤5 -1,25<y≤3,25
ИЛИ у∈(-1,25; 3,25].
№5
С(2а; 5)
4х - 5у = 15 подставим координаты т.С
4*2а - 5*5 = 15
8а=15 + 25
8а=40
а=5
тогда С(10; 5) ∈ прямой 4х-5у=15; проверим:
4*10 - 5*5=40-25=15
ответ: а=5.