а) график линейной функции, который параллелен заданной прямой, имеет тот же угловой коэффициент, что и заданная прямая, поэтому уравнение лин. ф-ции имеет вид : , то есть можно написать в ответ , или , или и т.д.;
Предположим, что утверждение верно для n=k. Покажем, и докажем, что утверждение верно так же для n=k+1. Так как , следуя предположению то прибавив к данному выражению d. Мы получим следующий член . Т.е. предположение верно. Ч.Т.Д.
2) База : 1 Проверка: .
Предположение:
Теперь покажем и докажем, что данное выражение верно и при :
Так как предыдущий член был равен k, то что бы узнать сумму первых k+1 членов, достаточно прибавить k+1 член (используя формулу которую мы доказали ранее): т.е. мы пришли к изначальной формуле, если туда подставить k+1. Ч.Т.Д.
3) Это не формула общего члена, это формула суммы. При получается деление на ноль, поэтому сразу пишем База: 1 Предположим, что формула верна для: Покажем и докажем что формула верна для : Как и с суммой арифм.прогрессии. Мы добавим k+1 член к сумме. Ч.Т.Д.
проверено.
![a_{k+1}=a_1+d[(k+1)-1]=a_1+dk](/tpl/images/0582/6750/35dc7.png)
![S_n= \frac{n[2a_1+d(n-1)]}{2}](/tpl/images/0582/6750/67d86.png)
. ![n=k \Rightarrow S_k= \frac{k[2a_1+d(k-1)]}{2}= \frac{2a_1k+dk^2-dk}{2}](/tpl/images/0582/6750/b9ca4.png)
:
получается деление на ноль, поэтому сразу пишем 
![b_{k+1}= \frac{b_1(1-q^k)}{1-q}+b_1q^k= \frac{(1-q)b_1q^k+b_1(1-q^k)}{1-q}\\= \frac{b_1[(1-q)q^k+(1-q^k)]}{1-q}= \frac{b_1[q^k-q^{k+1}+1-q^k]}{1-q}= \frac{b_1(1-q^{k+1})}{1-q}](/tpl/images/0582/6750/552be.png)
а) график линейной функции, который параллелен заданной прямой, имеет тот же угловой коэффициент, что и заданная прямая, поэтому уравнение лин. ф-ции имеет вид :
, то есть можно написать в ответ 
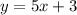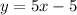, или 
, или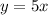 
и т.д.;
б) график , пересекающий график заданной функции, :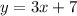
;
в) график, параллельный графику данной функции и проходящий через начало координат, имеет вид :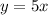
.