В числителе вынести х за скобку и получим
х(х^2-4х-5)
х-5 = 0
Решим кв. уравнение и разложим на множители числитель
х(х-5)(х+1)
х-5 = 0
Сократим (х-5)
х(х+1) =0
х=0, х=-1
В решении.
Объяснение:
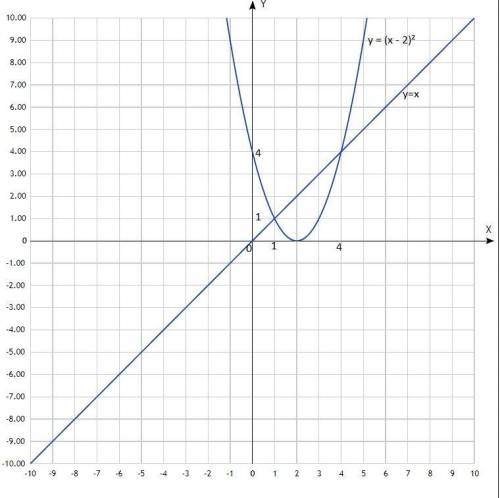
Решить графически систему уравнений:
y = (x - 2)²
y = x
Первый график - парабола со смещённым центром, второй - прямая, проходящая через начало координат.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
y = (x - 2)² y = x
Таблицы:
х -1 0 1 2 3 4 5 х -1 0 1
у 9 4 1 0 1 4 9 у -1 0 1
По вычисленным точкам построить графики.
Согласно построению, координаты точек пересечения: (1; 1); (4; 4).
Решения системы уравнения: (1; 1); (4; 4).
В решении.
Объяснение:
а) Преобразуйте выражение, чтобы получить многочлен стандартного вида. Укажите степень многочлена.
(2х² - 2)² - 4х³(х³ + х² - х - 2) + 4(х²)³ + 20х⁹/5х⁴ - 2(4х³ + 1) =
= 4х⁴ - 8х² + 4 - 4х⁶ - 4х⁵ + 4х⁴ + 8х³ + 4х⁶ + 4х⁵ - 8х³ - 2 =
= 8х⁴ - 8х² + 2. Стандартный вид. Степень (х⁴) = 4.
б) Докажите, что при любых целых значениях x многочлен делится на 2.
Так как коэффициенты при х чётные (8 и 8) и число 2 также чётное, при любых значениях х многочлен делится на 2.
в) Докажите, что при любых действительных значениях x многочлен не может принимать отрицательных значений.
Так как 8х⁴ > 8х² и степени при х чётные, то есть, сами одночлены в составе многочлена не могут быть отрицательными, при любых действительных значениях x многочлен не может принимать отрицательных значений.
x*(x^2-4*x^2-5x) = 0;
x ≠ 5;
x = 0;
x^2-4*x^2-5x = 0;
За теоремой Виета
x1 =-1;
x2 = 5;
x2 не подходит так как в знаменателе получиться 0