
ответ: 36 бусин.
Объяснение:
Так как всего бусин - 56 шт., а красных, зелёных и голубых - всего 11+18+19=48 шт., то чёрных и белых бусин вместе - всего 56-48=8 шт. Поэтому невозможно взять ни 10 чёрных, ни 10 белых бусин. В самом худшем случае сначала будут взяты все чёрные и белые бусины, затем - 9 красных, затем - 9 зелёных и потом - 9 голубых: тогда следующая бусина будет либо 10-й красной, либо 10-й зелёной, либо 10-й голубой. Таким образом, для гарантированного взятия 10 бусин одного цвета нужно взять 8+9+9+9+1=36 бусин.
Решение системы уравнений (5; 8)
Объяснение:
Решить систему уравнений методом сложения:
(х+3)/2 - (у-2)/3 =2
(х-1)/4 + (у+1)/3 =4
Умножить первое уравнение на 6, второе на 12, чтобы избавиться от дроби:
3(х+3)-2(у-2)=12
3(х-1)+4(у+1)=48
Раскрыть скобки:
3х+9-2у+4=12
3х-3+4у+4=48
Привести подобные члены:
3х-2у= -1
3х+4у=47
Умножить первое уравнение на -1, чтобы применить метод сложения:
-3х+2у=1
3х+4у=47
Складываем уравнения:
-3х+3х+2у+4у=1+47
6у=48
у=8
Теперь подставляем значение у в любое из двух уравнений системы и вычисляем х:
3х-2у= -1
3х= -1+2у
3х= -1+2*8
3х=15
х=5
Решение системы уравнений (5; 8)
Общий вид квадратного уравнения: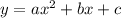 .
.
Количество корней квадратного уравнения зависит от дискриминанта D.