Доброй ночи товарищи. 2 системы уравнений 1)2x^2 - xy + 8y^2 = 32
x - 2y = -3
2) (2x - 5) (y + 3) = 0
4x^2 - 2xy + y^2 = 49

Question

Алгебра: Доброй ночи товарищи. 2 системы уравнений 1)2x^2 - xy + 8y^2 = 32 x - 2y = -3 2) (2x - 5) (y + 3) = 0 4x^2 - 2xy + y^2 = 49

dimas194 · Accepted Answer

Каноническое уравнение, задающее эллипс, выглядит так:

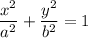
$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$

Перепишем уравнение эллипса, поменяв местами параметры и :

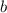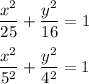
$\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\\\\\dfrac{x^2}{5^2}+\dfrac{y^2}{4^2}=1$

При этом мы получим конгруэнтный эллипс, только повёрнутый в системе координат на 90° (конгруэнтность следует из симметричности канонического уравнения). Поэтому он будет иметь тот же эксцентриситет и то же фокальное расстояние.

Найдём эксцентриситет:

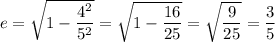
$e=\sqrt{1-\dfrac{4^2}{5^2}}=\sqrt{1-\dfrac{16}{25}}=\sqrt{\dfrac{9}{25}}=\dfrac{3}{5}$

Найдём фокальное расстояние (полурасстояние между фокусами):

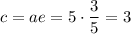
$c=ae=5 \cdot \dfrac{3}{5}=3$

Тогда расстояние между фокусами в два раза больше: 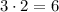$3 \cdot 2=6$ .

ответ: 6 ед.

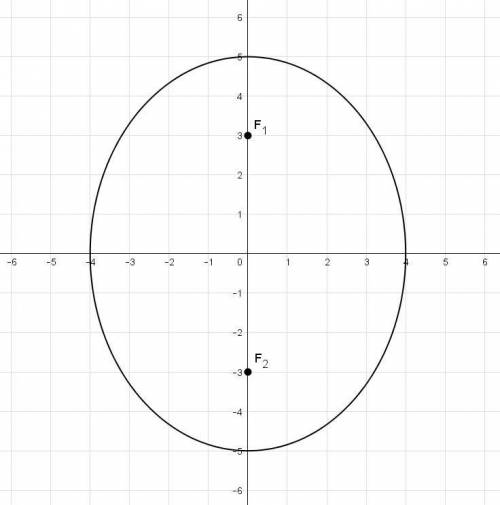
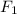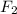На чертеже изображён данный эллипс. F_1 и F_2 — его фокусы.

Найти расстояние между фокусами эллипса<img src=

" />

Доброй ночи товарищи. 2 системы уравнений 1)2x^2 - xy + 8y^2 = 32 x - 2y = -3 2) (2x - 5) (y + 3) = 0 4x^2 - 2xy + y^2 = 49

MOGZ ответил

Доброй ночи товарищи. 2 системы уравнений 1)2x^2 - xy + 8y^2 = 32
x - 2y = -3
2) (2x - 5) (y + 3) = 0
4x^2 - 2xy + y^2 = 49