ДАНО: f(x) = x² - 4x + 3.
Пошаговое объяснение:
Это парабола с ветвями вверх. Для того чтобы найти её вершину преобразуем уравнение к полному квадрату.
x² - 4*x + 3 = (x² -2*x*2 + 2²) - 4 + 3 = (x - 2)² - 1.
Прибавили и отняли 2² = 4.
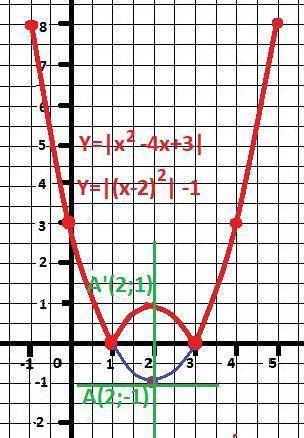
Получаем координаты вершины параболы - точки А(2;-1).
Но отрицательную часть графика надо отразить относительно оси ОХ - в точку A'(2;1).
Парабола четная и симметричная. Построение по точкам - относительно прямой Х = 2.
x = y = 1
x = 1, 3, y = 0
x = 0, 4, y = 3
x = -1, 5, y = 8
у = 5х + 1 - ((6х-3)/х) = 5х + 1 - 6 + (3/х) = 5х - 5 + (3/х).
Так как переменная есть в знаменателе, то график такой функции - гиперболическая кривая.
Найдём производную этой функции.
y' = 5 - (3/x²) и приравняем её нулю.
5 - (3/x²) = 0.
(5x² - 3)/x² = 0. Достаточно приравнять нулю числитель.
5x² - 3 = 0.
x² = 3/5.
x = +-√(3/5).
Имеем 2 значения точек экстремума. Подставим их в функцию и находим 2 значения:
у = -5 + 2√15 ≈ 2,7459667,
у = -5 - 2√15 ≈ -12,745967.
В этих точках касательная к графику параллельна оси Ох и функция достигает предельных значений.
Получаем область допустимых значений функции:
x ≤ -12,745967, x ≥ 2,7459667.
Эти же значения можно записать так:
x ≤ -5 - 2√15, x ≥ -5 + 2√15.