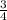
-p(4+p) +(p-2)(p+2) = -4p -p²+p²+2p-2p-4 = -4p -4
при р= 3/4
-4•3/4 - 4 = -3-4 = -7
(x+1)(x^2-x+1)-x(x+3)(x-3) Упростим данное выражение, для этого раскроем скобки. Также заметим, что (x+1)(x^2-x+1) - это формула сокращенного умножения: a³+b³=(a+b)(a²-ab+b²) , где, в нашем случае, a - это x, а b - это x, таким образом, (x+1)(x^2-x+1)=x³+1.
Заметим, (x+3)(x-3) - тоже формула сокращенного умножения - разность квадратов
(x+3)(x-3)=x²-9/ Преобразуем наше выражение, дораскрываем скобки:
(x+1)(x^2-x+1)-x(x+3)(x-3)=x³+1-x(x²-9)=x³+1-x³+9x=9x+1.
Найдем значение выражение при x=1:
9*1+1=10.
Удачи!
Сначала упростим выражение:
-p(4+p)+(p-2)(p+2) = -4р - р^2 + р^2 - 4 = - 4р - 4
Теперь подставим значение р
-4 × 3/4 - 4 = - 3 - 4 = -7