
Введем обозначения:
k - площадь, занятая кукурузой
a - площадь, занятая овсом
p - площадь, занятая пшеном
x - свободная площадь
S - площадь всего поля
По условию, если свободную часть поля полностью засадить пшеном, то пшено будет занимать половину всего поля. Но тогда и кукуруза вместе с овсом будут тоже занимать половину поля. Получаем равенства:
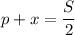 (1)
(1)
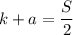 (2)
(2)
По условию, если свободную часть поля поровну поделить между овсом и кукурузой, то овёс будет занимать половину всего поля. Но тогда и кукуруза вместе с пшеном будет занимать половину поля. Получаем равенства:
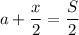 (3)
(3)
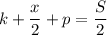 (4)
(4)
Составим выражение, которое будет отвечать на вопрос задачи. Если свободную часть поля отдать под кукурузу, то она будет занимать площадь 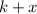 , хотя до этого она занимала площадь
, хотя до этого она занимала площадь 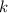 . Соответственно, площадь увеличилась в
. Соответственно, площадь увеличилась в 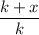 раз.
раз.
Значит, нужно найти связь между k и x.
Заметим, что правые части уравнений (1)-(4) равны. Удобно приравнять левые части (2) и (3) уравнения, так как в них кроме переменных k и x встречается только переменная a, причем в одинаковом выражении, которое впоследствии взаимно уничтожится:
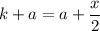
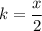
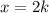
Подставим в искомое выражение:
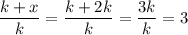
ответ: в 3 раза
1) Найдем нулю нашей функции. Для чего разложим на множители формулу, которой она задана, с введения новых вс членов.
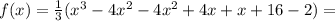
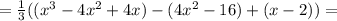
![=\frac{1}{3}[x(x-2)^{2}-4(x-2)(x+2)+(x-2)]=](/tpl/images/0065/5986/78255.png)
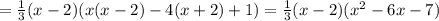
Из 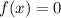 следует:
следует:
а) 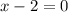 , отсюда
, отсюда 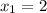 - нуль функции
- нуль функции
б) 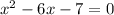 ,
, 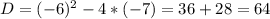 , отсюда
, отсюда
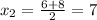 ,
, 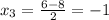 - нули функции
- нули функции
Итак, функция 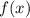 обращается в нуль в точках
обращается в нуль в точках 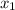 ,
, 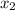 и
и 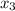
2) Найдем возможные точки экстремума нашей функции. Для чего найдем производную функции 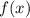 :
:
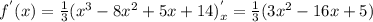 -----(1)
-----(1)
Разложим квадратный трехчлен, стоящий в правой части (1), на целые множители. Для чего найдем дискриминант этого квадратного трехчлена:
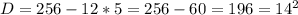 , отсюда найдем корни:
, отсюда найдем корни:
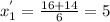
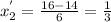 ---------(2)
---------(2)
Тогда с (2) выражение (1) примет вид метода интервалов найдем промежутки, на которых производная функции 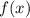 принимает положительные и отрицательные значения:
принимает положительные и отрицательные значения:
а) 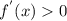 при x принадлежащем объединению промежутков
при x принадлежащем объединению промежутков
(-бесконечности; 1/3)U(5; +бесконечности )
б) 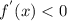 при x принадлежащем промежутку (1/3; 5)
при x принадлежащем промежутку (1/3; 5)
Известно, что промежутки, на которых производная функции положительна, являются промежутками возрастания функции!
На промежутках, где 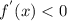 , функция убывает!
, функция убывает!
Поскольку при переходе через точку x=1/3 производная меняет знак с плюса на минус, то эта точка - точка максимума
Поскольку при переходе через точку x=5 производная меняет знак с минуса на плюс, то эта точка - точка минимума. Итак,

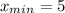
1.х - аргумент; у - функция; подставляйте
2.Просто подставляем в формулу известное и находим неизвестное.
Если известен х, то у находим по формуле
у = -12/x
А если известен у, то находим х по формуле
х = -12/y
1). х = -600
у = -12/(-600) = 0,02
2). у = 0,1
х = -12/0,1 = -120
3). х = -12
у = -12/(-12) = 1
4). х = -0,05
у = -12/(-0,05) = 240
5). х = 0,5
у = -12/0,5 = -24
6). у = -1
х = -12/(-1) = 12
7). х = 120
у = -12/120 = -0,1
8). у = -0,02
х = -12/(-0,02) = 600