
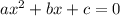
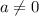 , так как уравнение обращается в линейное.
, так как уравнение обращается в линейное.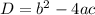
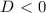 уравнение не имеет решений (вообще имеет, но это в школе не проходят).
уравнение не имеет решений (вообще имеет, но это в школе не проходят).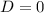 то уравнение имеет 1 решение (корень).
то уравнение имеет 1 решение (корень).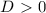 - уравнение имеет 2 корня.
- уравнение имеет 2 корня.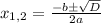
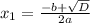
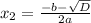
 ,
, , a
, a 
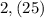
 целая часть. У нас она равна 2
целая часть. У нас она равна 2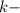 - количество цифр в периоде. У нас их 2
- количество цифр в периоде. У нас их 2 количество цифр до периода. У нас их 0
количество цифр до периода. У нас их 0 все цифры, включая период, в виде натурального числа. У нас это 25
все цифры, включая период, в виде натурального числа. У нас это 25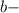 все цифры без периода в виде натурального числа. Их нет.
все цифры без периода в виде натурального числа. Их нет.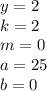
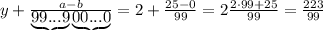
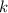 подставляется количество 9, а под
подставляется количество 9, а под  -количество нулей. У нас
-количество нулей. У нас 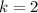 , значит пишем две цифры 9, а
, значит пишем две цифры 9, а  , значит, нулей не пишем вообще. Между
, значит, нулей не пишем вообще. Между 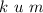 не стоит знак умножения
не стоит знак умножения
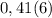
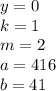

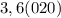

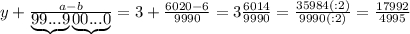
b=2; b=-2
Объяснение:
ОДЗ:
b=/=5
b=/=-5
Дробь равна 0, если ее числитель
равен 0, а знаменатель =/=0.
==>
Числитель дроби приравниваем
нулю:
Применяем формулу разности
квадратов:
не подходит, так как b=/=5
Дробь равна 0, если
b=2
b=-2